How to Teach Fractions on a Number Line

Understanding fractions on a number line

Despite the fact that there is an increasing consensus in educational research that number lines are the most effective instructional representation for fractions, and curricula are increasingly making them an emphasis, number lines are consistently hard to teach. There are a number of reasons for this, but they can be summed up in a simple statement: fraction number line instruction requires a high degree of just-in-time feedback to be effective, especially for struggling students. In a traditional classroom setting, it’s next to impossible to provide this level of instruction because the teacher can’t be everywhere at once.

 
What are effective instructional techniques for teaching with number lines?

Given the difficulties of teaching this topic in a traditional classroom, teachers often (and understandably!) feel limited and frustrated in their ability to teach fractions on a number line effectively. While there’s no magical solution to the difficulties inherent in teaching fraction number lines, a few instructional techniques can mitigate them.

 
Number line basics #1: Start small and go slow

Number lines are difficult for students. Period. Children need a lot of time and practice successfully creating and reading fractional representations to develop reliable accuracy on various problems.

While there’s a natural temptation to see “how far you can get” with your students in a single lesson, it’s not a good idea. Number lines are a tool students use to learn several important and fairly complex concepts. Learners must be able to interpret number line representations with high fidelity and fluidity, which is only developed with repeated practice.

What’s the upshot? When first learning how to read fraction number lines, it is far better to give students multiple successes on more straightforward problems. For instance, 20-30 exercises like the below example will allow students to form increasingly solidified neural pathways around the number line representation.

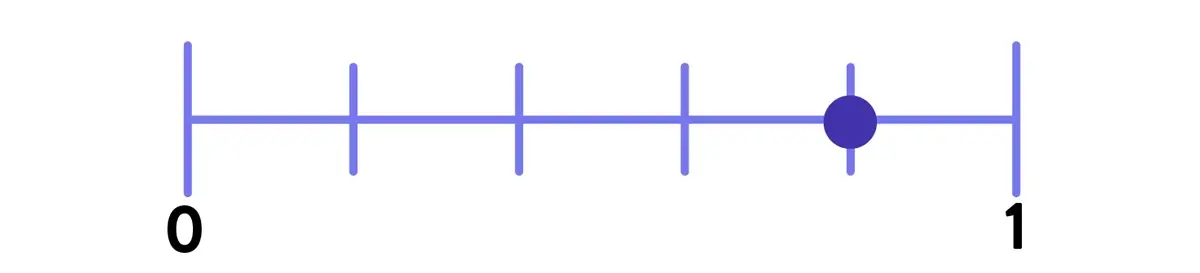
On the other hand, introducing unnecessarily difficult or visually dense representations (like this example below) – before a student is confident with the number line itself – will only create “cognitive noise” and confusion. This may slow a student’s progression towards mature number line work and cost you valuable instructional time.

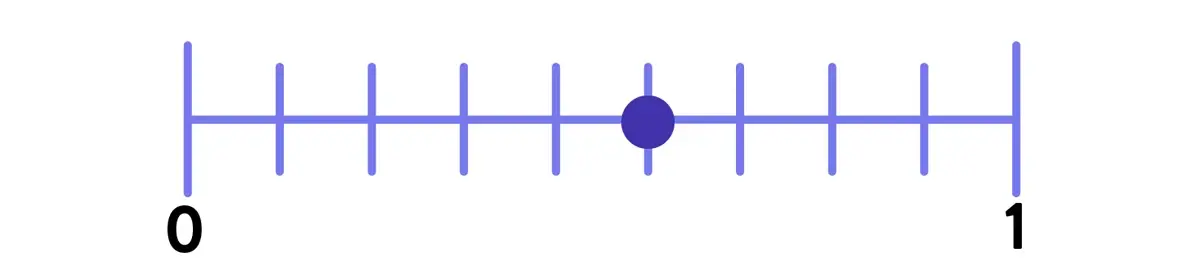
Bottom line: brain-based education teaches us that “practice makes permanent.” Make sure your students practice the right thing with the correct conceptualization before moving on to more complex or challenging material.

 
Number line basics #2: Teach students to count intervals, not tick marks

One of the main points of confusion when teaching fractions on a number line is the relationship between the denominator value and the number of tick marks. Does the following number line represent thirds or fourths?

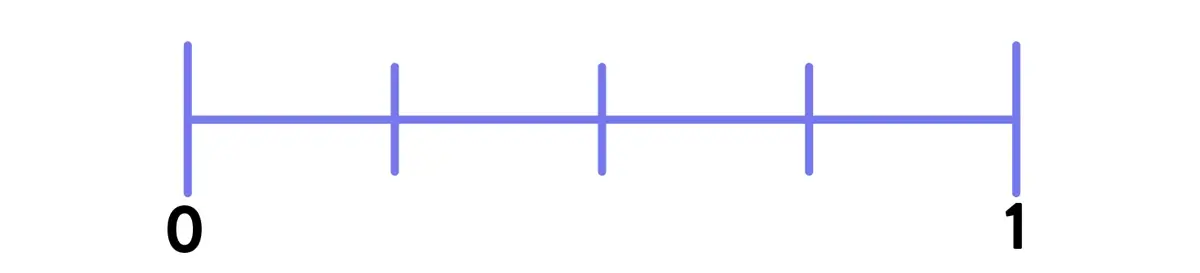
For someone familiar with the representation, it’s clear that the number line above represents fourths – there are four intervals between 0 and 1. However, for a student who is still transitioning from the predictable world of integer number lines to the far-less-predictable world of fraction number lines, the answer is not so clear.

The tick marks are what “jump off the page” visually, so it’s completely understandable that a student would see three tick marks and think: “3… that’s thirds!”

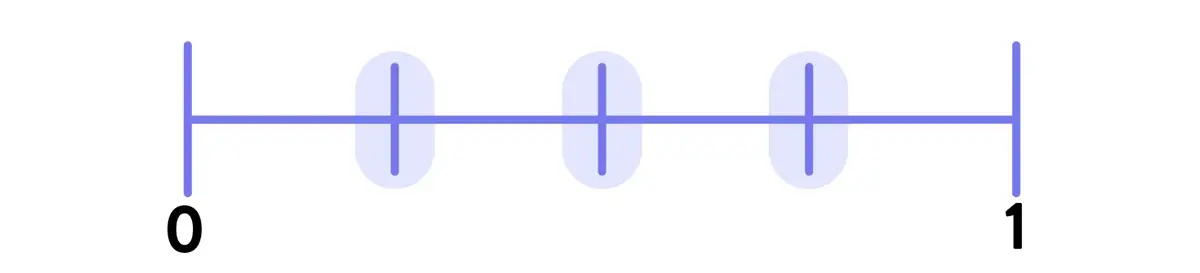
Of course, you can teach tricks like: “add 1 to the number of tick marks between 0 and 1.” However, using this trick – as with many shortcuts in math – obscures the underlying conceptual reality that makes the number line so powerful. That is, the number line shows partitions of the space between 0 and 1 in the same way that a shaded area model shows partitions of a shape that represents 1… all without the inconvenient aspects of shaded area models (see below).

You need to train your students to look for the intervals – the actual space or distance on the number line – rather than the tick marks that divide that space.

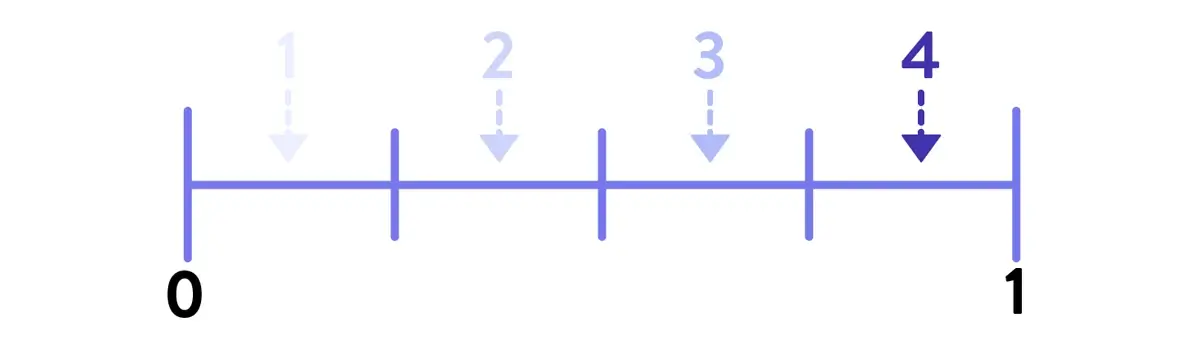
Once students have learned to do this reliably, much of the difficulty surrounding number lines evaporates, unlocking the potential for learning in this powerful representation.

 
Number line basics #3: Incorporate fractions >1 as soon as possible

For many students, fractions are “easy” until they start representing quantities greater than one. At that point, metaphors like “equal sharing” become more difficult. “Share a pizza equally four ways… and then give a piece to five different people.” That's not so easy to understand...

Part of what makes the number line representation effective at building strong fraction number sense is that fractions greater than one are completely intuitive. No convoluted explanations are necessary about how you can have more pieces than a whole – fractions greater than one are just another point on the number line!

Mixing problems that require the student to work with fractions greater than one into your early instruction will help your students build surprisingly strong number sense without much fanfare. You will be amazed at the dividends this pays when you compare mixed numbers and fractions greater than one!

Here’s a teaser: Which is bigger, ⁷/₃ or 2 ²/₃ ? No mixed number conversion is required!

 
Number line basics #4: Structure your lessons to minimize the time between a student error and corrective feedback

As mentioned above, teachers tend to spend little time on number line content mainly because learning to use the number line effectively is feedback-intensive. It requires a very short gap in time between a student’s mistake and a corrective piece of feedback. Otherwise, the student may wind up inadvertently cementing erroneous ways of interpreting or working with the representation.

Any math teacher will tell you that teaching students to unlearn a given method or misconception is ten times more difficult than teaching something for the first time. We need to get number line instruction right from the beginning for our students; otherwise, a vicious cycle can occur.
 

 
The only way to prevent this cycle from starting is never to allow it to begin in the first place.

Unfortunately, doing so requires the nearly impossible: the teacher needs to be immediately available to each student as they learn and make mistakes. When the student begins counting tick marks, the teacher must immediately redirect them to count intervals instead. When a child incorrectly counts all intervals between 0 and 2 to find the denominator value of a fraction >1, they need to be immediately redirected to count only the intervals between 0 and 1.
 

There are no magic solutions to this problem. However, some approaches can help.

1. Carefully craft student pairings when doing number line lessons.The goal is to ensure that students who are already proficient can provide feedback to students who are still building proficiency.

   Unfortunately, this is often impractical or impossible. When you first introduce the topic, few students will already know enough material that they can be relied on to give accurate feedback. Students take a long time to develop their proficiency, so it will be a while before a teacher can reliably count on them to help their peers.

2. Design lessons that allow for small group instruction. Math “center time” can be helpful – have the majority of the class complete self-directed activities while you work with a small group of students, where you can immediately intervene when they make mistakes or verbalize misconceptions.

   Ensuring that you have enough time dedicated to such lessons is vital. Students need a lot of practice to cement their conceptual understanding and build effective strategies for working with number lines. Only one or two of these small-group times before “moving on” will significantly increase the danger of that vicious cycle setting in for many of your students.

3. Utilize technology tools that allow the entire class to work simultaneously on number line skills. The benefit of an online resource for this topic is that it allows all students to receive just-in-time feedback as needed. If the program is well-designed, students will get the gentle scaffolding and immediate feedback they need to become proficient users of this powerful number line tool.

   It’s essential that you find an appropriate, effective tool for this instructional practice. Not all online resources are created equally, and a platform that doesn’t provide appropriate feedback or adapt to a student’s growing proficiency – or recurring difficulties – will be hardly better than paper and pencil work (at best) and counterproductive (at worst).

 
Frax is a powerful online tool that builds fraction number line skills in a very short time

ExploreLearning Frax is demonstrated to help students (grades 3+) build robust fraction skills in a remarkably small amount of time.

From Day 1, students work with fractions as numbers in an intuitive setting as they associate a fraction’s value with the length of a block model. With Frax, students seamlessly transition to the number line representation, with an emphasis on understanding the space between 0 and 1 and counting intervals to determine the denominator value.
 

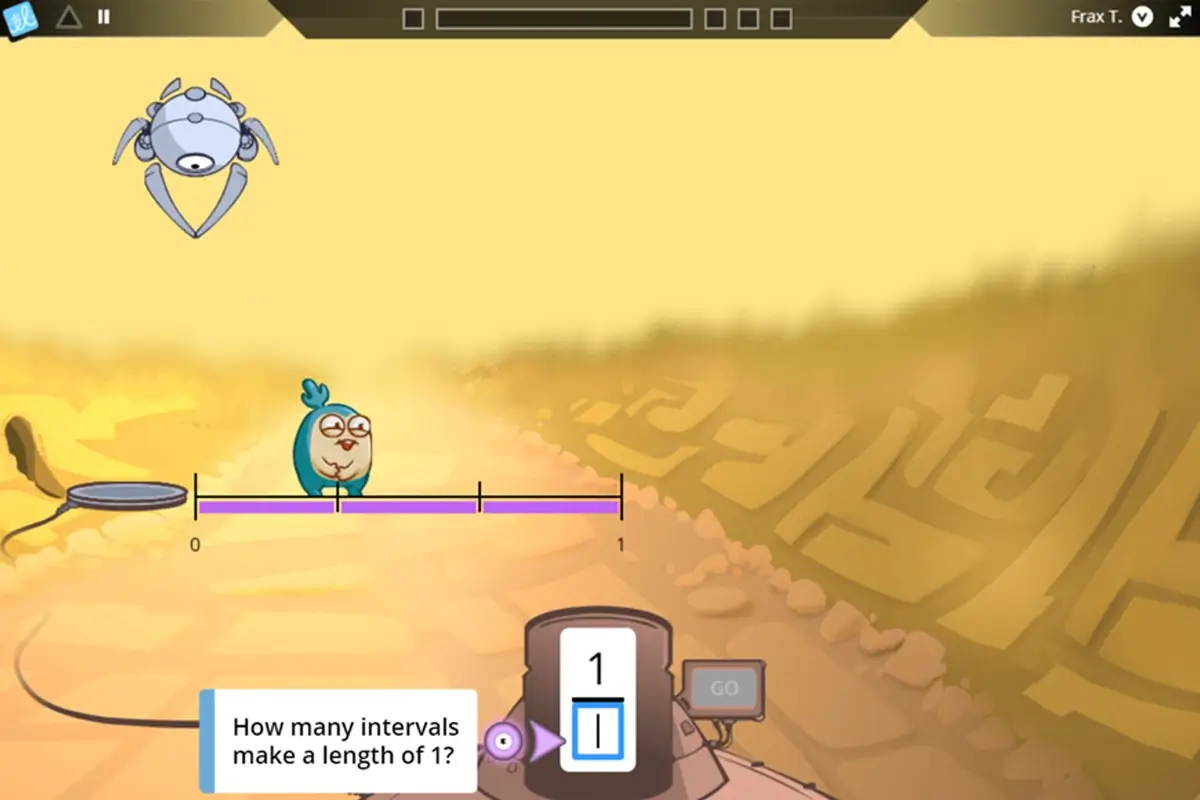
Space-themed games and engaging lessons help students build confidence and competence in fraction number line representations, with adaptive logic ensuring they only see questions they are ready to tackle.

 
 Students read points on a number line…

 
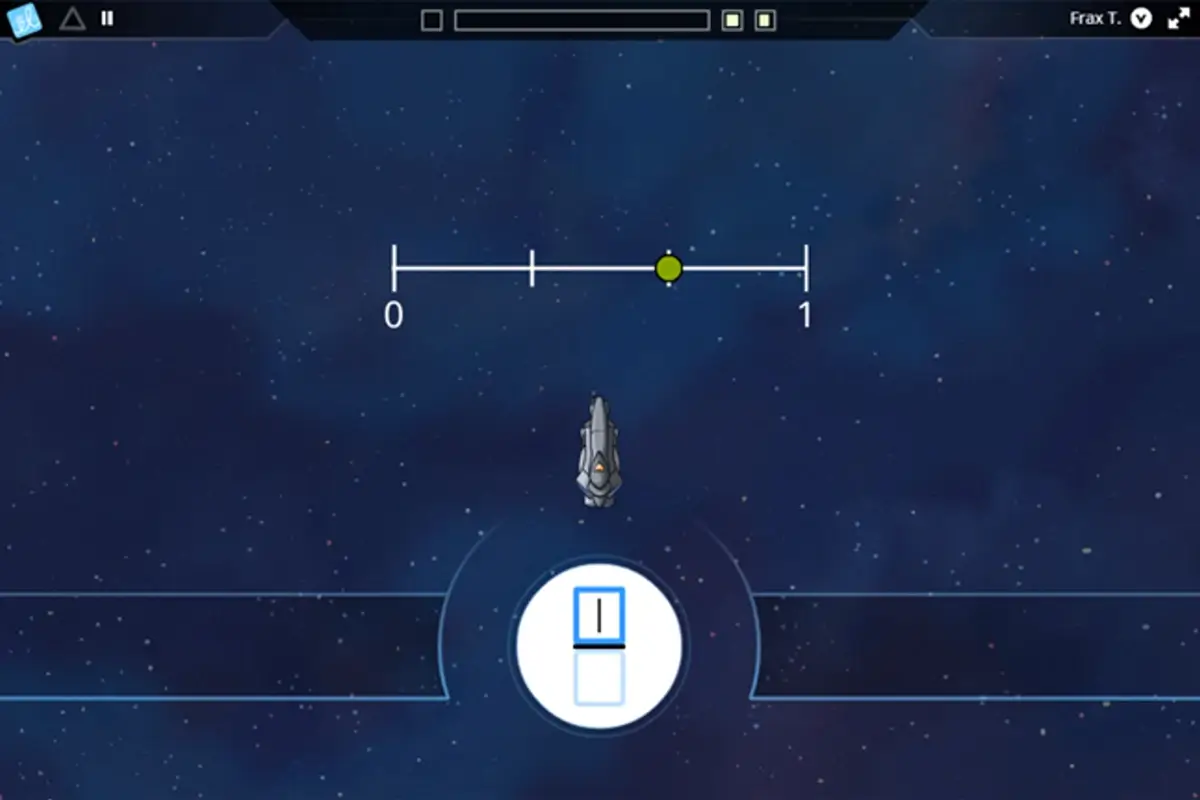
 … and place points on number lines.

 
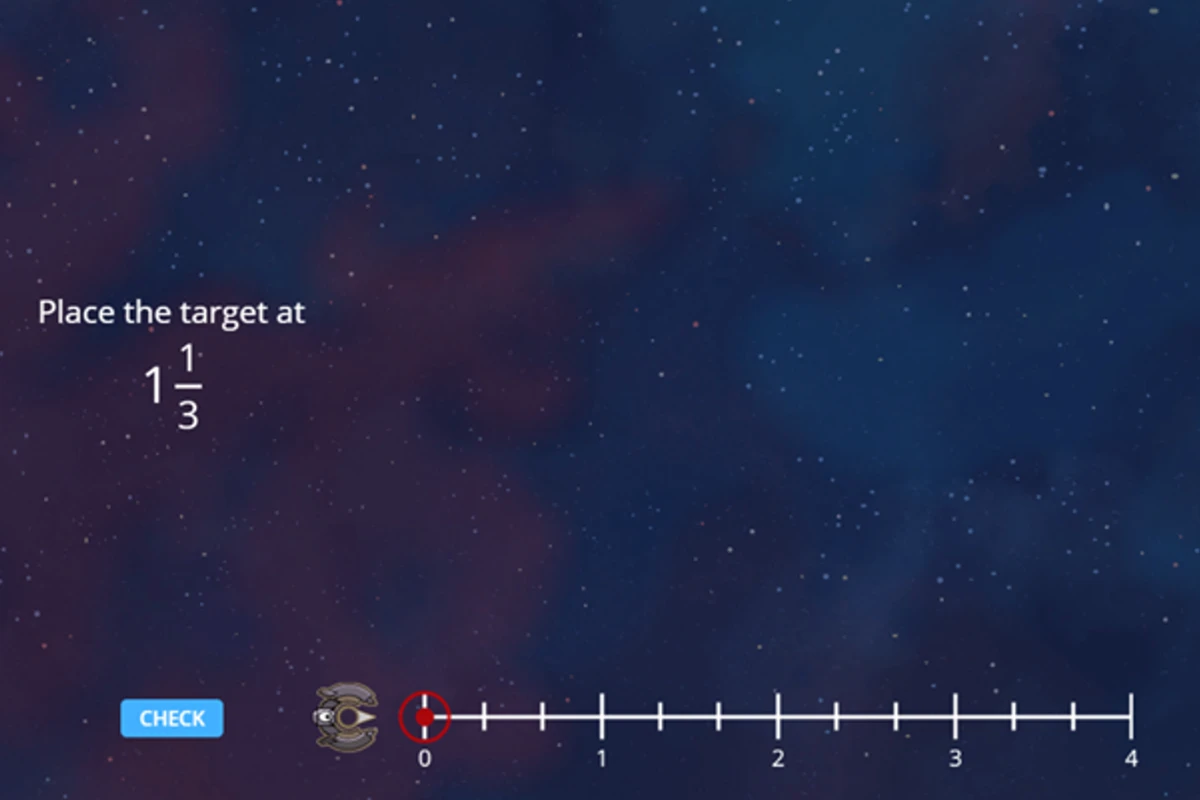
 Students create number lines themselves…

 
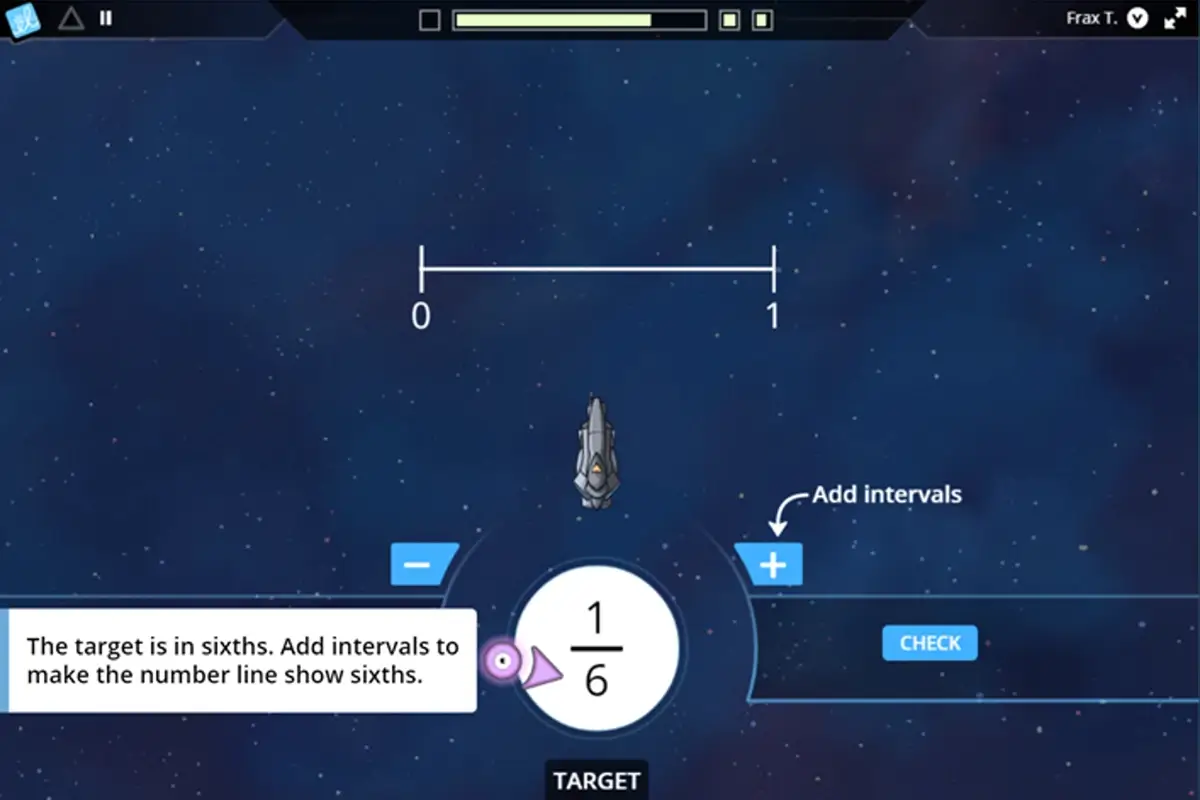
 …and estimate fraction and mixed number locations on unmarked number lines. 

 
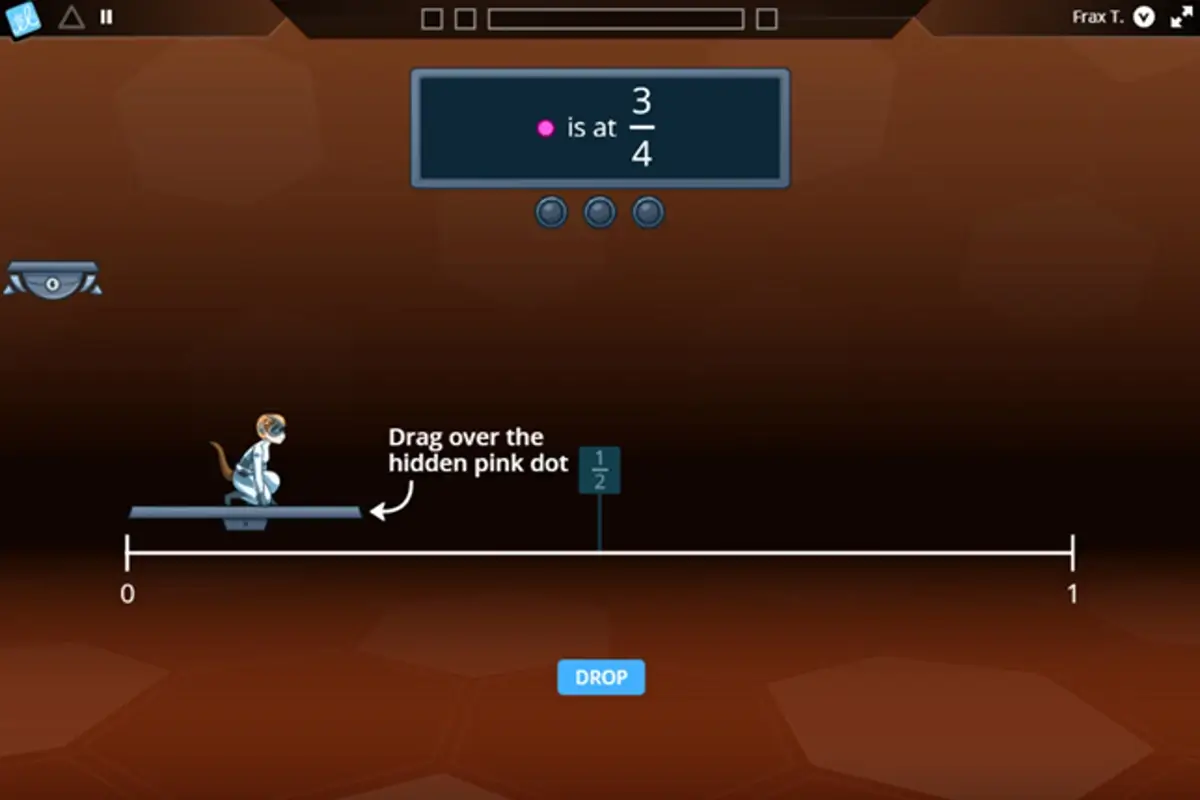
These skills are embedded throughout the Frax student experience, so even when the curriculum focuses on a different topic, students still receive the practice they need to solidify their understanding and skills.
 

 Try Frax