Converting Mixed Numbers to Fractions Greater Than 1

What are mixed numbers and fractions greater than 1?

When a student encounters a mixed number like 2 5/6 they can easily apply their foundational knowledge to convert the mixed number to a fraction greater than 1. But how? Keep reading to discover practical steps and classroom applications to try today. 

Mixed numbers defined

Mixed numbers are numbers that include both a whole number and a proper fraction. For example, 2 5/6 represents two wholes and 5/6 of another whole, making the mixed number very close to the whole number 3.

What is a fraction greater than 1?

Fractions greater than 1 have a numerator that is larger than their denominator. Since fractions are numbers too, they can be greater than one (just like any “regular” number). For example, 6/6 is equivalent to 1. If students count by sixths on a number line, they encounter 7/6, 8/6, and beyond. All of these are fractions greater than one.

You might also hear the term improper fractions in your curriculum or textbook to describe fractions with a greater numerator than the denominator. Address this term with students in case they encounter it on assessments, but there is no need to emphasize it during instruction. Once students understand that fractions are numbers, it becomes natural to understand that numbers (including fractions) can be greater than one.

How to convert mixed numbers to fractions greater than 1

To convert a mixed number into a fraction greater than 1, students must first change the whole number to an equivalent fraction. 

Take the mixed number 2 5/6. The whole number 2 needs to be converted into a fraction. Students know that 6/6 is equivalent to 1 and apply that knowledge to multiply 2 wholes by 6/6 (equivalent to 1). Doing so converts the 2 into the same original value, but now in a fraction represented by sixths = 12/6.

In the all-new Frax Sector 3, students practice converting mixed numbers to fractions greater than 1 in a game-based environment. In the Cell Splitter game, students rewrite mixed numbers using tools they’ve already developed from Sectors 1 and 2.

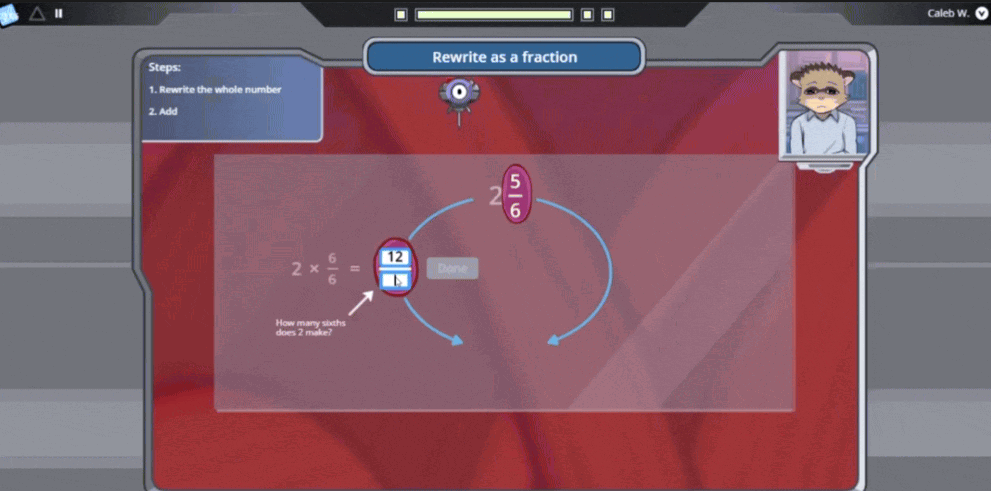
After rewriting the whole number 2 as a fraction with the same denominator (12/6), students simply add to find the fraction greater than 1. In this case, the student adds 12/6 + 5/6 to find 17/6, the fraction greater than 1. Remind students that 17/6 is equivalent to the mixed number they started with, 2 5/6.

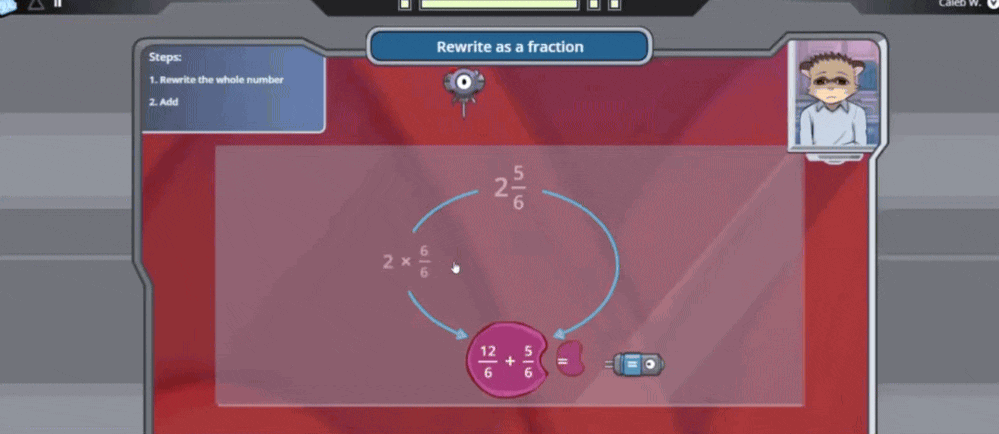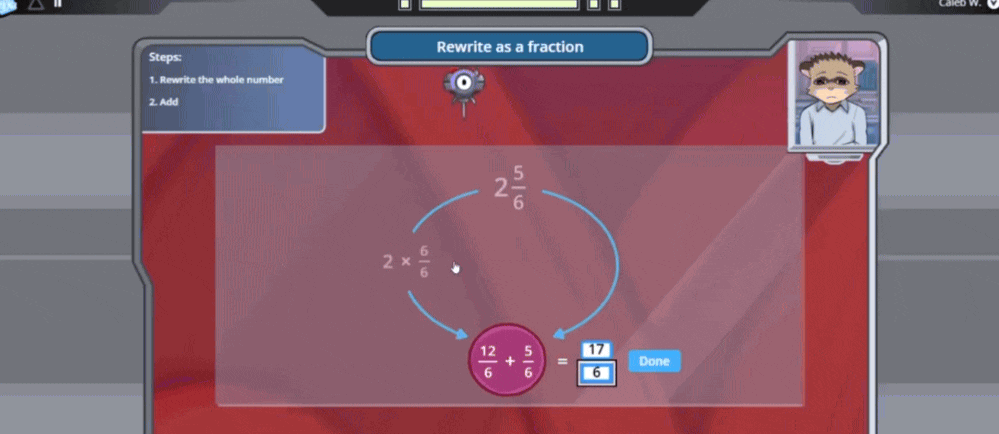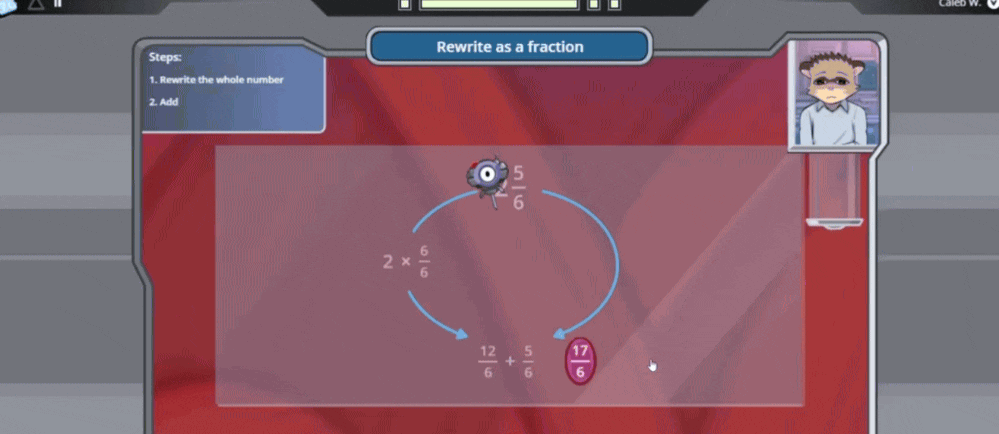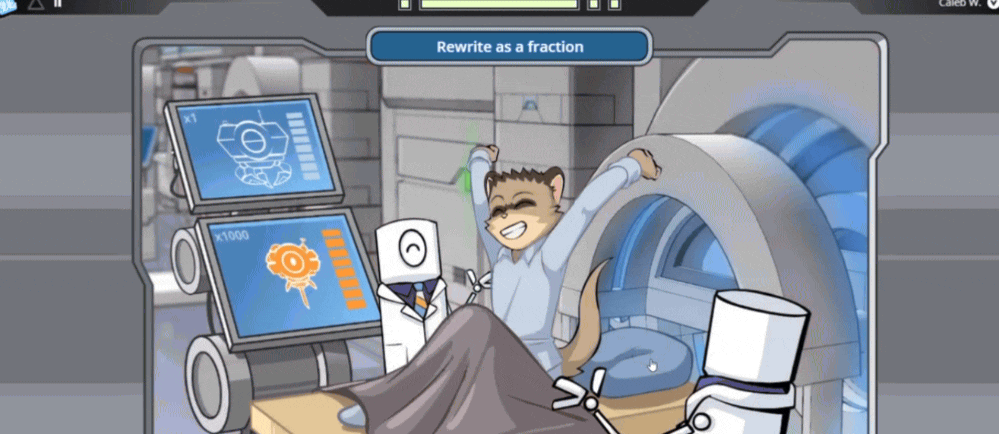
Understanding how to convert mixed numbers helps students flexibly move between representations of fractions greater than 1. When teaching fraction conversion tips, emphasize that the denominator stays the same—it represents the size of the parts.

Tips for teaching this concept in the classroom

Teaching fractions greater than 1 can be a fun (and rewarding) opportunity to help your students build a deeper understanding of fractions. 

Try these classroom-tested strategies:

• Use visual models, such as length models, number lines, fraction bars, or shaded area models, to illustrate the connection between wholes and parts.
• Encourage students to explain their reasoning out loud. Talking through their thinking out loud helps students solidify understanding.
• Point out the "big ideas" of fractions whenever they come up in discussion. For example, the "big idea" is that any fraction of the form n/n equals 1. This is always the key to converting between a whole number and a fraction.

When you teach fractions from a foundation of conceptual understanding, you help students see fractions as numbers, rather than memorizing a strict set of rules to follow. Remind students to check their work by converting the fraction greater than 1 back to a mixed number to see if the result matches the original problem.

Use Frax to help students master fractions

Frax takes the struggle out of teaching fractions by giving students a strong conceptual foundation through interactive, game-based learning. The research-based and adaptive design ensures that every student builds fluency with fractions, including fractions greater than 1.

Using research-based strategies, visual models, engaging games, and scaffolded practice, Frax helps students move beyond memorization to a true understanding of fractions, including fractions greater than 1.