
What are equivalent fractions?
Equivalent fractions are two different fractions that have the same value. Think of them as different ways of measuring the same length!
For instance, the pink “gas cow” is 1 1/2 in. long, right?
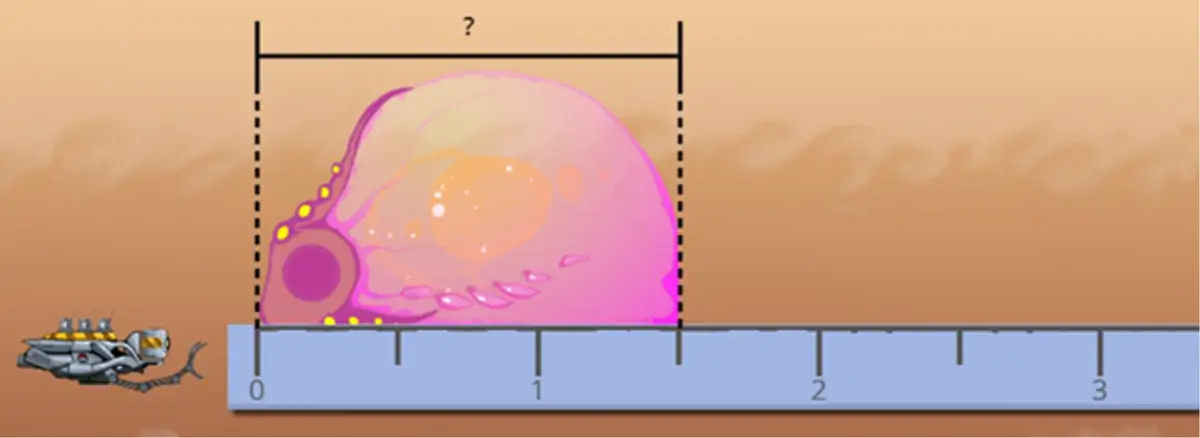
But the same gas cow is also 1 2/4 of an inch long if the ruler uses these marks:
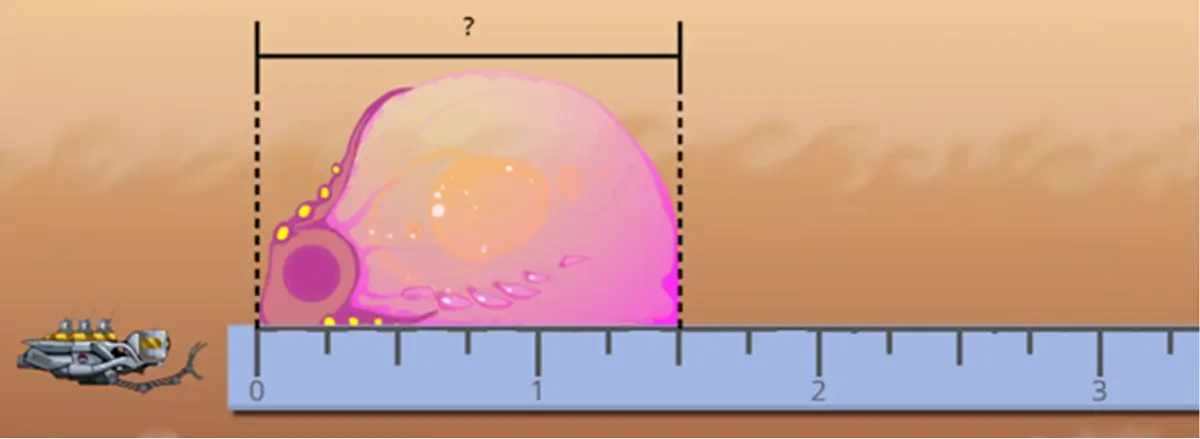
And it’s also 1 4/8 of an inch long if your ruler is even more fine-grained:
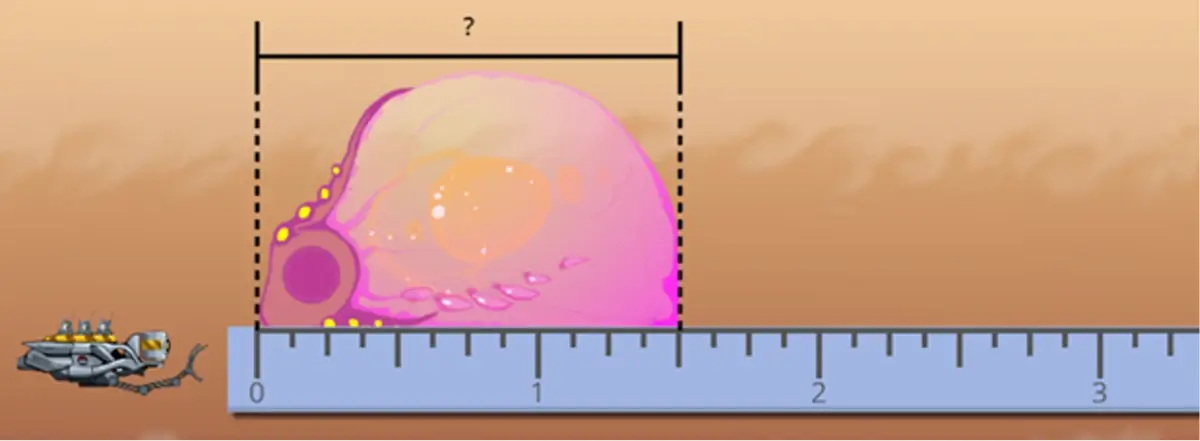
The same object (with the same length) can be measured and written in many different ways. Each of those ways is an equivalent fraction to the other.
Why are equivalent fractions important?
Think about it – what makes fractions unique in the world of numbers? In most ways, fractions are just like every other number: you can point to them on the number line, compare their size to other numbers, and add, subtract, multiply, and even divide them.
However, one of the unique things about fractions is that they can be rewritten using equivalence. 1/2 can be rewritten as 2/4, 4/8, or even 50/100. Four different fractions that all live at exactly the same place on the number line! This ability to change in form without changing in value is very useful when it comes to adding and subtracting fractions with different denominators. You can’t make common denominators without knowing how to use equivalent fractions! Equivalent fractions are also helpful for comparing two fractions with different denominators. For instance, it’s hard to look at 7/9 vs. 2/3 and have a clear, intuitive sense of which one is bigger. But if you know that 2/3 is equivalent to 6/9, your comparison just got much easier! 7/9 is clearly bigger than 6/9 because it has more ninths.
Effective teaching strategies
What’s the best way to teach equivalent fractions? There are many ways to help students understand the concept of equivalence, but they all start with students understanding that fractions are just like any other number. That is, you can find a single place on a number line where a fraction “lives.”
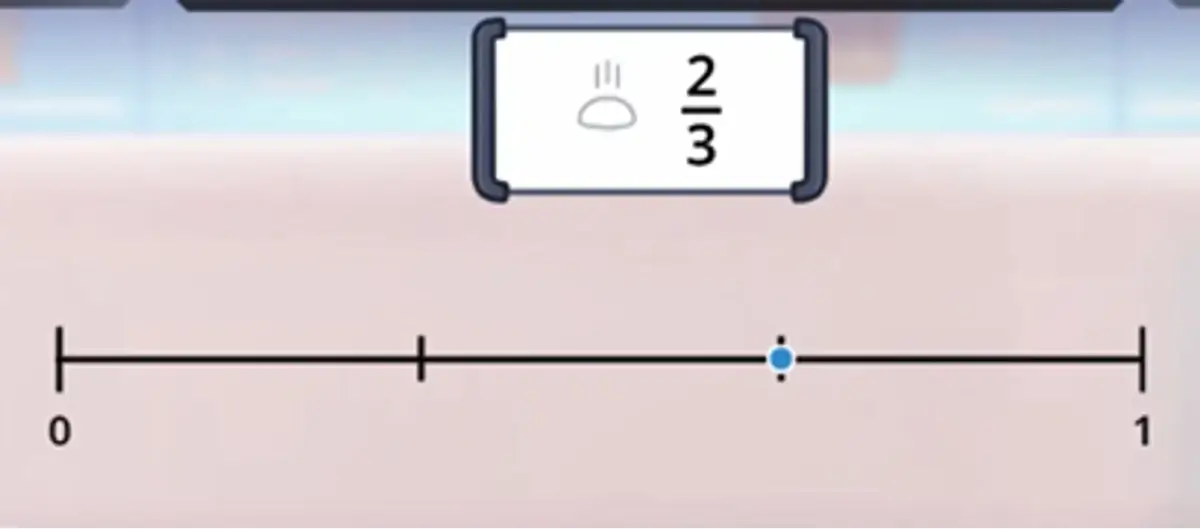
Or you can create a model of how long that fraction is:
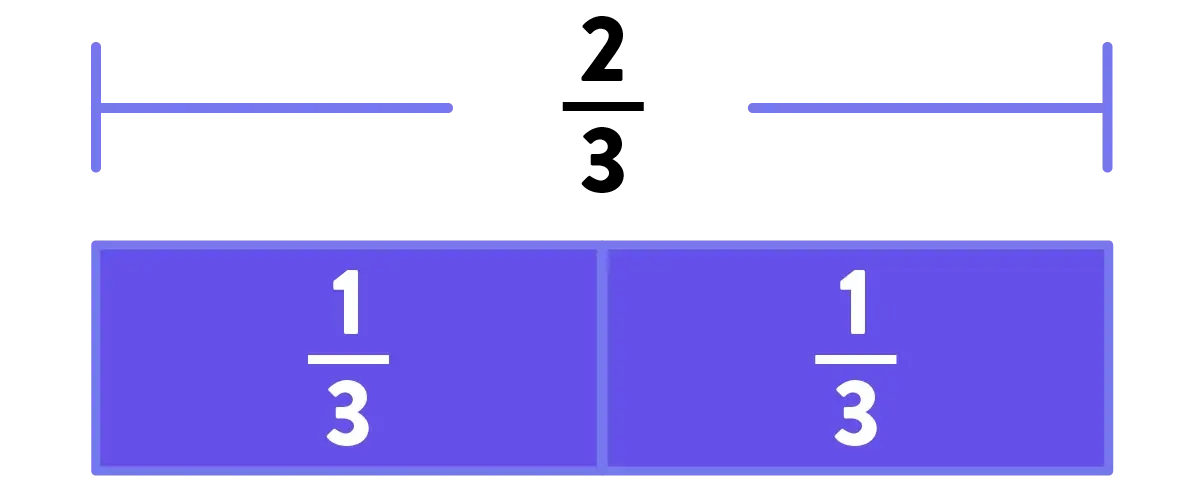
Using those same models, you can show how equivalent fractions are either at the same location on the number line…
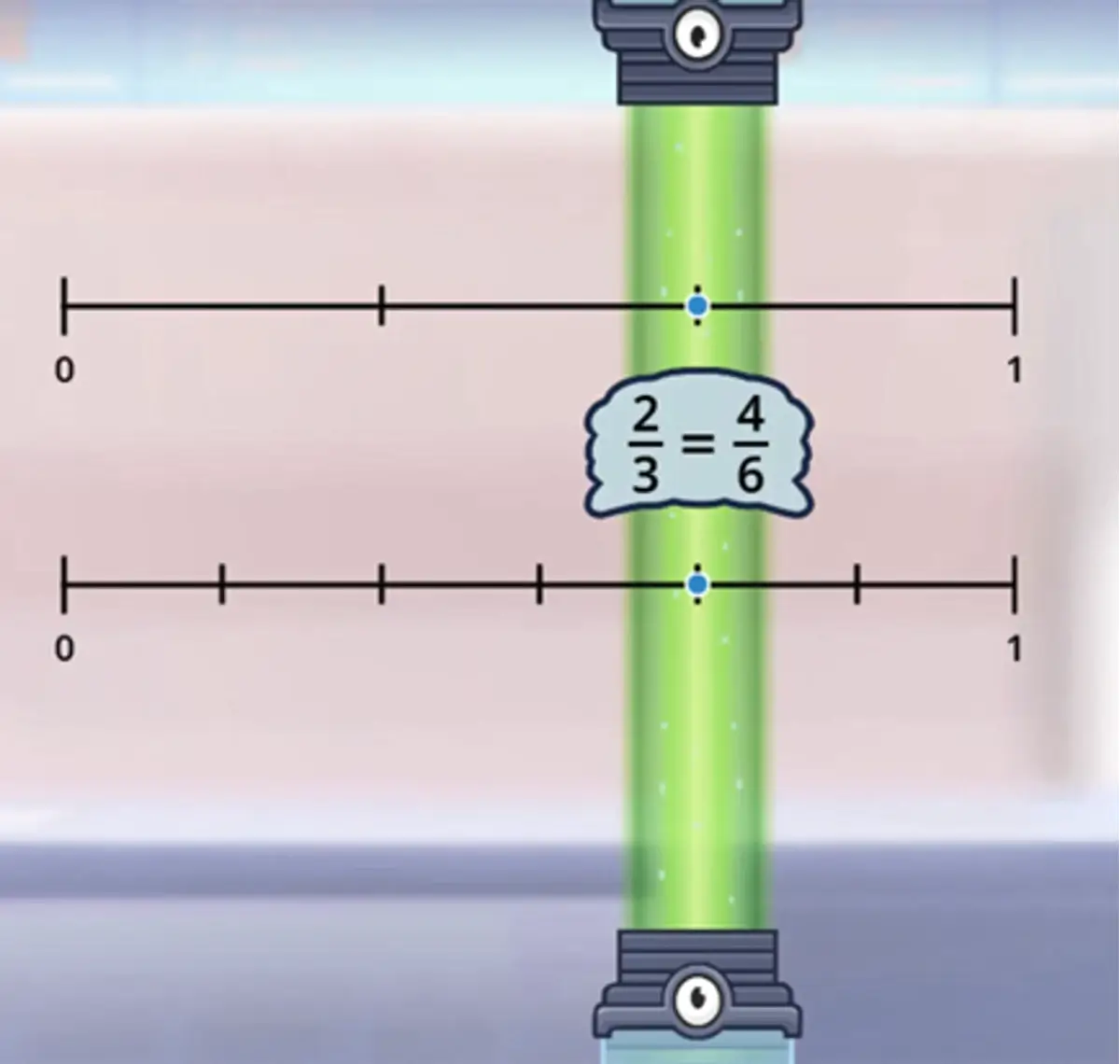
…or that they have the same length when represented as block models.
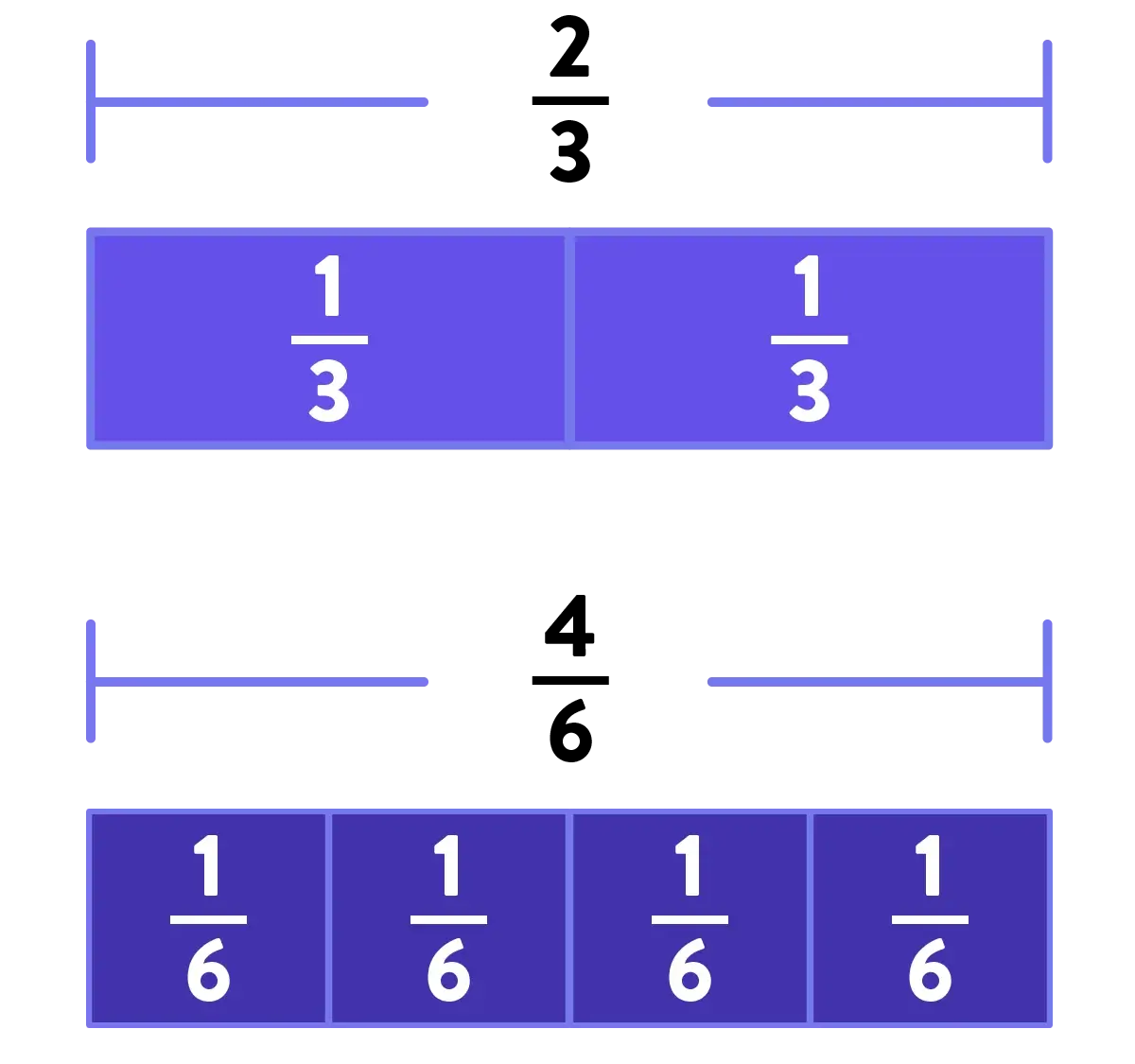
Anchoring your instruction around something concrete and visual, like “two ways of saying the same point on a number line” or “two ways of saying the same length of a block model,” makes equivalent fractions feel intuitive and easy to students.
Why do shaded area models limit fractions equivalence practice?
Teachers often use shaded area models (like “pie models”) as the primary way to teach equivalence. While these are helpful to a point, they can also be limiting for students if they’re the only model used to teach equivalent fractions. Why?
Notice how much less intuitive the following diagrams are compared to the number line and block models above.
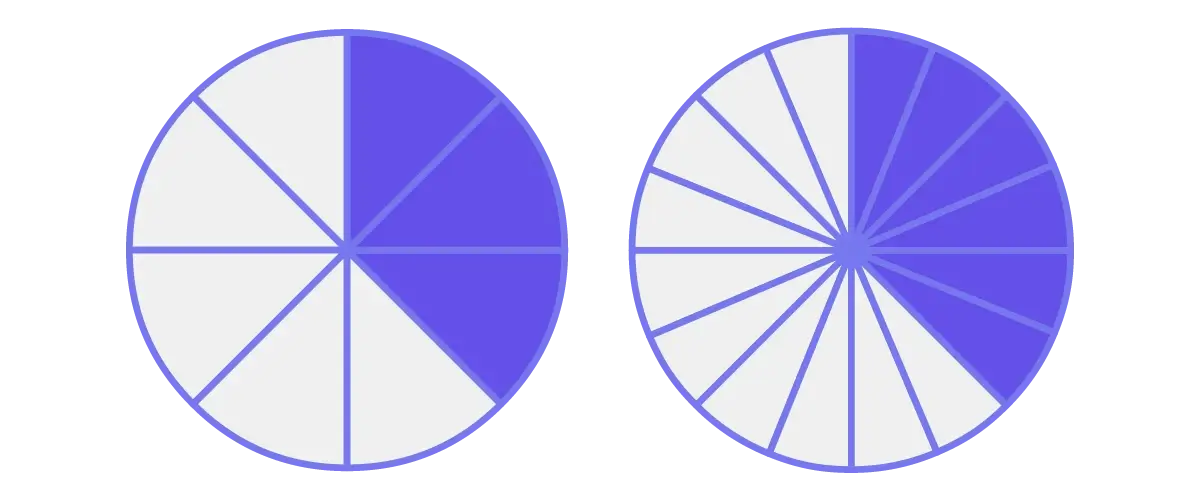
Two numbers with larger denominators make it much harder to see the equivalence intuitively. It’s much more difficult to see that these models represent the same area at a glance. You must spend time, attention, and mental energy visually comparing them. Not to mention the fact that if the right-hand model were 5/16 instead of 6/16, you might not immediately notice the difference!
The fact that shaded area models are much less clear at a glance than number lines or block models means you have to use a lot more mental energy and attention to prove to yourself that they are the same area. This is not easy for many students, and it unnecessarily distracts from the big-picture concept you’re trying to convey: equivalent fractions have the same length/area even though they’re written differently.
Also, shaded area models can’t help your students build a robust concept of fractions as numbers, each with their own value and unique location on the number line!
Teach equivalent fractions with Frax
With ExploreLearning Frax, students (grades 3-5) master fractions while having fun playing research-driven, galaxy-themed games.
All of the examples above (with the exception of the circle models) came directly from Frax. They demonstrate Frax’s incremental, model-based approach to building students’ understanding of how fractions are just like any other number with a length and a location on the number line.
Frax doesn’t just talk about or show how numerators and denominators work in tandem to communicate a fraction’s length or position – students complete tasks and play games so they can dynamically see and feel that concept. Over time and with practice, students build robust mental representations of fractions as lengths. This means that when it comes time to learn about equivalence, the notion of “two different fractions with the same length” is completely intuitive.
In Frax, the instruction leverages various models (number lines, block models, and shaded area models), as well as fractions presented only in their numeric form. Ultimately, students learn to create equivalent fractions to match a specified denominator, and then they use that skill to make difficult comparisons between unlike fractions. They also use their growing equivalent fractions skills to measure lengths accurately and begin to add unlike fractions in the context of decimals.
Frax just got even more fun!
Introducing Frax Competitions! Compete with other classrooms in your school and watch motivation soar. This new feature lets students face off with other classes in their school to stay engaged and build fraction skills.
Teachers trust Frax because it works
In a recent study, more than 99.7% of educators reported improvements in student learning and engagement using Frax, while 87% considered Frax a better program than any previously utilized to teach fractions. Teachers also noted increased student participation, self-esteem, and learning thanks to the platform.
When researchers compared the gains produced by Frax to other interventions, the standardized effect sizes revealed that Frax was 3x more effective than the average educational intervention for 3rd-graders and 5x more effective for 4th-graders.
Frax meets students at their level with frequent rewards, just-in-time instruction, and game-based fun. Frax also supports teachers with student reporting, pre-made offline resources, professional development, and community with other educators.

Everybody's Talking About Frax
“Frax is a fantastic supplement to our math curriculum. Students are able to more easily and quickly grasp complex concepts such as equivalent fractions and comparing fractions with different denominators.”
-Teacher. Albuquerque Public School Dist School District, NM“I like how Frax breaks down learning to a deeper level. It shows that fractions with different denominators can be equivalent with more or less pieces. This is extremely helpful for 4th grade because there’s a big emphasis on equivalent fractions.”
-Teacher. Allen Park Public School District, MI“My students love using Frax. They love the graphics and how it feels like video games with different missions. My students are engaged and have a better understanding of fractions and equivalent fractions.”
-Teacher. Colquitt County School District, GAAbout the Author

Jesse Mercer, Senior Product Designer at ExploreLearning
Jesse Mercer, a Senior Product Designer at ExploreLearning, has over 20 years of experience in education and related fields. He has an MA in Math Education, is a National Board Certified teacher for secondary mathematics, and was a recipient of his district’s “Golden Apple” award for teaching. During his 13 years in the classroom, Jesse taught upper elementary and middle school mathematics courses, ranging from 5th-grade math through Algebra I. He currently works with several other designers on creating the curriculum and instructional content for Frax.
