Strategies to Help Algebra Make Sense for Students

Algebra is built on a small set of potent tools called properties or axioms. We can all state them with ease. The commutative, associative, distributive, and identity properties, plus a small handful of others, cover the real number system. Add in the properties of equality, and you have the basic toolset that will support students well in their journey through and beyond high school algebra.

As any algebra teacher can also tell you, many students view algebra as anything but simple and powerful. ‘Confusing’ and ‘painful’ are words that might more quickly come to mind. Why? Part of the issue is surely related to how proficient they are with fractions, decimals, integers, and basic arithmetic. Students who struggle in these areas are going to see their troubles compounded when they are faced with them in the context of more advanced new content. Another significant part of the problem, though, is rooted in the way we teach the material.

The trouble with certain approaches to teaching algebra

We often teach the properties of real numbers and equality as facts to be memorized rather than tools to be utilized. We teach them and quiz students on them, but when it comes time to get down to work with algebraic expressions, we tend to shift gears, relying instead on a series of techniques detached from the properties that underlie them. We “gather like terms” without reference to the distributive property that makes this possible. When we want to multiply two binomials, we “FOIL.” Solving a proportion is easy – just “cross multiply.” Pretty soon, the algebra student begins to see math as a series of unrelated tricks and techniques that have no connection to the algebraic properties or any math that came before.

These approaches to teaching have been around for a long time because, to a certain extent, they work. Many students have long accepted that math doesn’t always make sense and are more than happy to use any technique that reliably gives the correct answer. In addition to meeting a student’s desire to have a reliable path to correct answers in a new topic, time limitations and the fact that most of us were taught using these same techniques means many of us never examine their limitations and explore alternatives. Many might also ask, if these approaches work, is this really a problem that needs solving?

The issue with these approaches is that they have a significant long-term cost. For many students, math pretty quickly becomes a “grab bag” of memorized techniques and tricks rather than a cohesive whole that makes sense. How many of us have seen kids with two fractional expressions near each other incorrectly decide that the best thing to do is to cross multiply? A lot of us. This is because cross-multiplication never made sense to them in the first place. It wasn’t taught to make sense. It was taught to get correct answers to the problems we were teaching at the time. So what was once a quick way to help kids solve proportions is now a liability, just one more unmoored technique in a confusing ocean littered with them. With the passage of time, each “trick” is either largely forgotten or occasionally (and sometimes inappropriately) pressed into action by a fuzzy memory of what it is good for.

A new approach for algebra readiness

Fortunately, new approaches are emerging to help students gain the foundation they need to make working with algebraic expressions and equations make sense. For example, in ExploreLearning’s interactive Equivalent Algebraic Equations Gizmo, students are immersed in a casual puzzle game environment in which they solve algebraic challenges to advance, gain stars, and earn higher ranks. What sets the games apart, though, is that the tools students use to achieve their goals are the algebraic properties themselves, coupled with a clear focus on big ideas.

In the Gizmo, the first in a two-part algebraic expressions series (check out Equivalent Algebraic Expressions II), students are focused on equivalent algebraic expressions. Students are first given a rigorous introduction to equivalence in the guise of basic training for new workers at the undersea “Equivalence Eatery.” This training is run by the cantankerous octopus chef, Theodore Grumpy. By the time they have finished this early experience, students have demonstrated that they understand what equivalence is and how to disprove equivalence by giving a counterexample. After that, the new trainees are off and running.

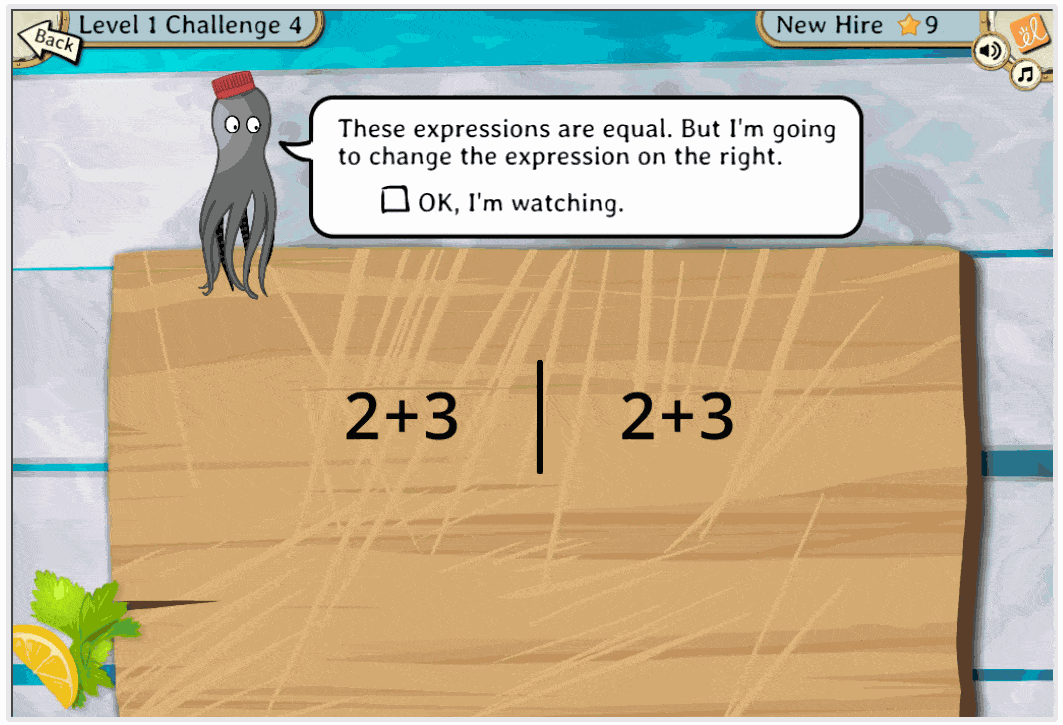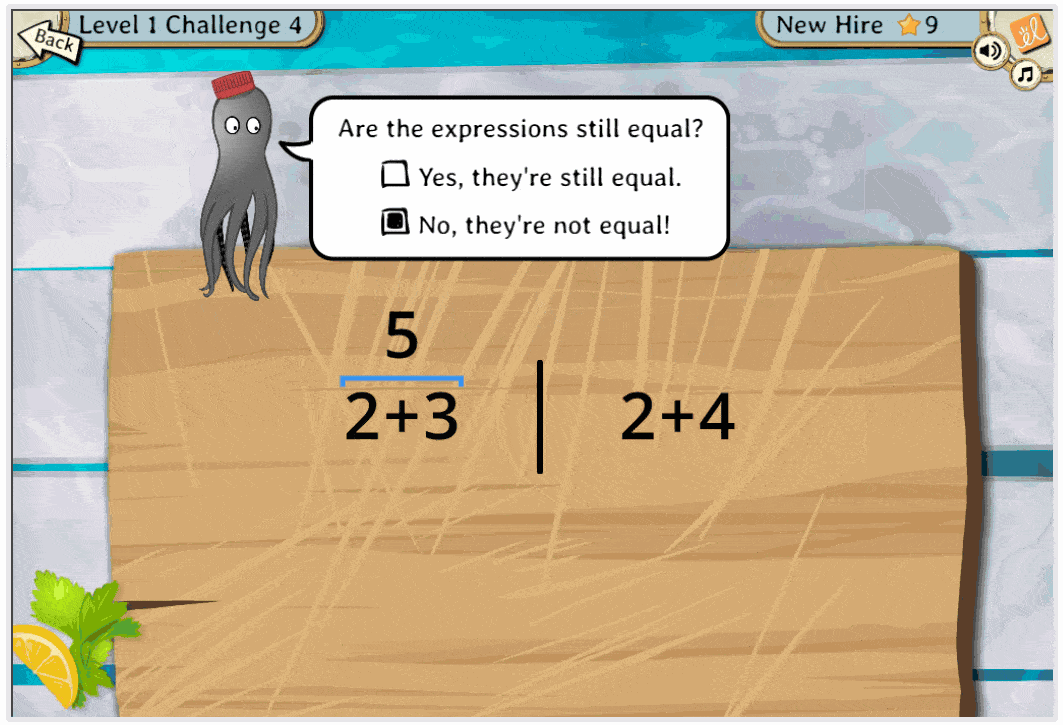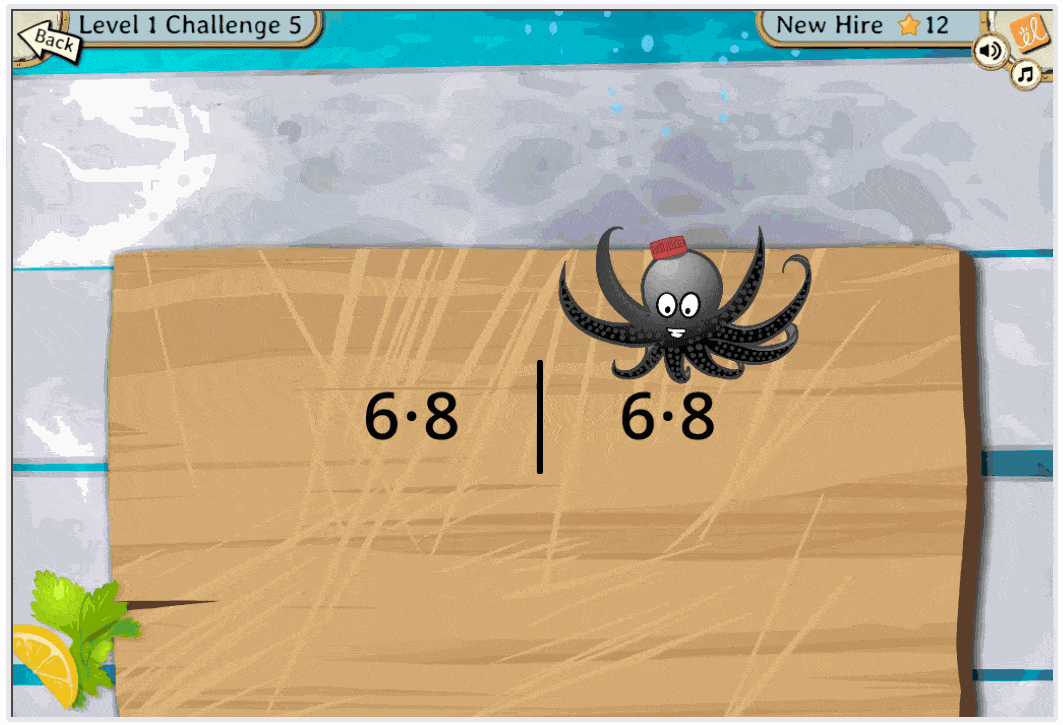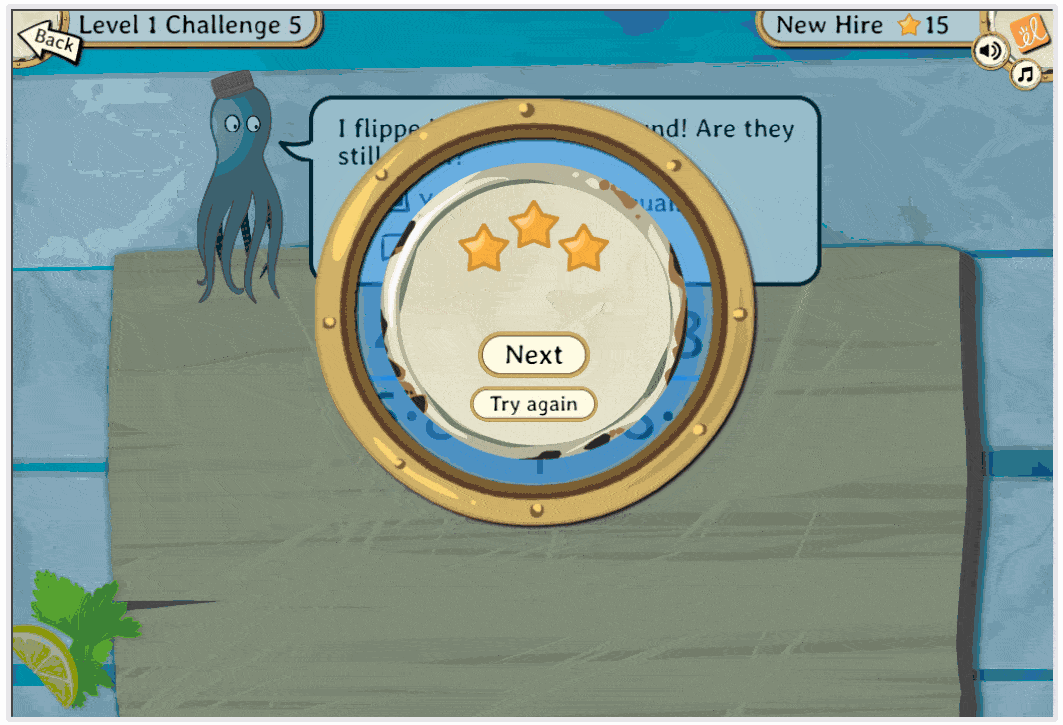
As they progress through the game, students utilize a growing set of new algebraic tools to overcome a series of challenges. Along the way, they learn the associative, commutative, and distributive properties and use them to rewrite algebraic expressions in different but equivalent forms. They learn to use the distributive property to both expand and factor, to rewrite subtraction as addition (and division as multiplication) so that they can use their powerful new tools more broadly. They practice making and justifying claims of equivalence or nonequivalence. In the process, algebraic properties become the means by which they make algebraic steps, not just an after-the-fact justification. The properties become the practical bedrock of how the students work with algebraic expressions.

Fractions in algebra: Unlock algebra success with a focus on fractions

Fractions are students’ first exposure to abstraction in math, and fractions proficiency is crucial for algebraic thinking used in advanced math courses. In a national study analyzing multi-year data, fractions knowledge at age 10 was the strongest predictor for math achievement at age 16. Yet, many students struggle with fractions, from conceptual understanding to more complex topics, resulting in a widespread lack of algebra readiness. 

Strong fractions instruction, which helps students understand fractions as numbers that can be rewritten, can actually prepare students well for the abstraction of algebra. Adaptive and game-based, ExploreLearning Frax (grades 3+) uses the latest evidence-based research and instructional methods to create a better way to learn fractions. Frax builds on intuitive visual representations (like length models) to introduce students to the number line representation of a fraction, helping them build a strong understanding of fraction magnitude (size), essential to later success in algebra.

Engage students with Gizmos and Frax for effective learning

Students are a tough audience when it comes to math. If a game is uninteresting or if onscreen interactions with mathematics are clunky, unintuitive, or inefficient compared to paper, they will quickly get frustrated and lose interest. So the team at ExploreLearning has worked hard to develop ways to easily and mindfully manipulate mathematical expressions and equations.

With Gizmos, press a “+” sign, and you have the option to add, commute, or associate the two addends. Press the “Commute” button, and the two terms quickly and smoothly rotate around the addition sign to switch places. All the interactions and animations are designed to reinforce when and how a property applies and then to clearly illustrate how the selected property transforms the expression. We’ve found that students using these Gizmos tend to display an unusual level of enthusiasm, perseverance, and even competitiveness in their work. Consequently, they are able to accomplish a great deal of systematic learning and practice in a relatively short period of time.

Using Frax, fractions feel like fun as students progress through carefully scaffolded instruction organized into missions. Each Frax mission features space-themed activities, customized characters, music, and enticing visuals that help students remain motivated and engaged as they build a conceptual understanding of fractions.

Inspire future scientists and mathematicians

Our mission at ExploreLearning is to help students think like and see themselves as future scientists and mathematicians. A big part of this mission is to help make math make sense to them. So we’re really excited to help teachers do this more easily with our latest series of Algebra Gizmos. Together, we can strip math down to its essential core and build up a new generation of more confident, conceptually grounded, successful students who will be ready to take on whatever comes next when they leave our classrooms.