How to Overcome 3 Challenges to Develop a Stronger Understanding of Fractions

A deep understanding of fractions is fundamental for future math success, but classroom instruction isn’t always as easy as pie. If you’ve found yourself frantically searching online for tips for teaching fraction concepts, you’re not alone. Learning and teaching fraction concepts come with their fair share of challenges for both teachers and students. Teaching with a focus on conceptual understanding of fractions will reduce the struggle and help students progress further in math.
We’ve identified three common misunderstandings that limit students’ understanding of fractions. How can you and your students conquer these common barriers to develop a robust conceptual understanding of fractions? Read on to discover three effective solutions!
Fractions misunderstanding #1: Thinking “bigger denominators make bigger fractions”
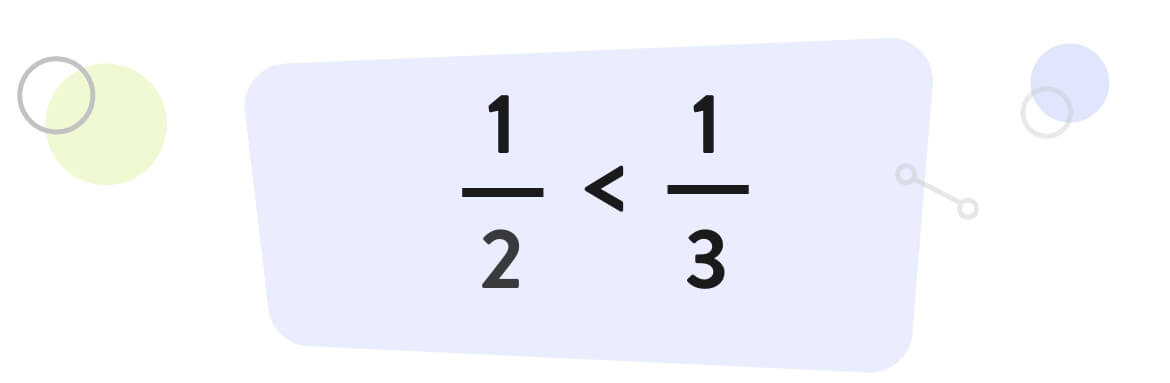
A common misconception when comparing fractions with numerators of 1 is believing that the fraction with the larger denominator value is the bigger fraction. In the example below (1/2 vs. 1/3), students might assume that 1/3 is greater in size than 1/2 because 3 is more than 2.
Common misconception:
Fractions teaching solution #1: Understanding the value of the denominator
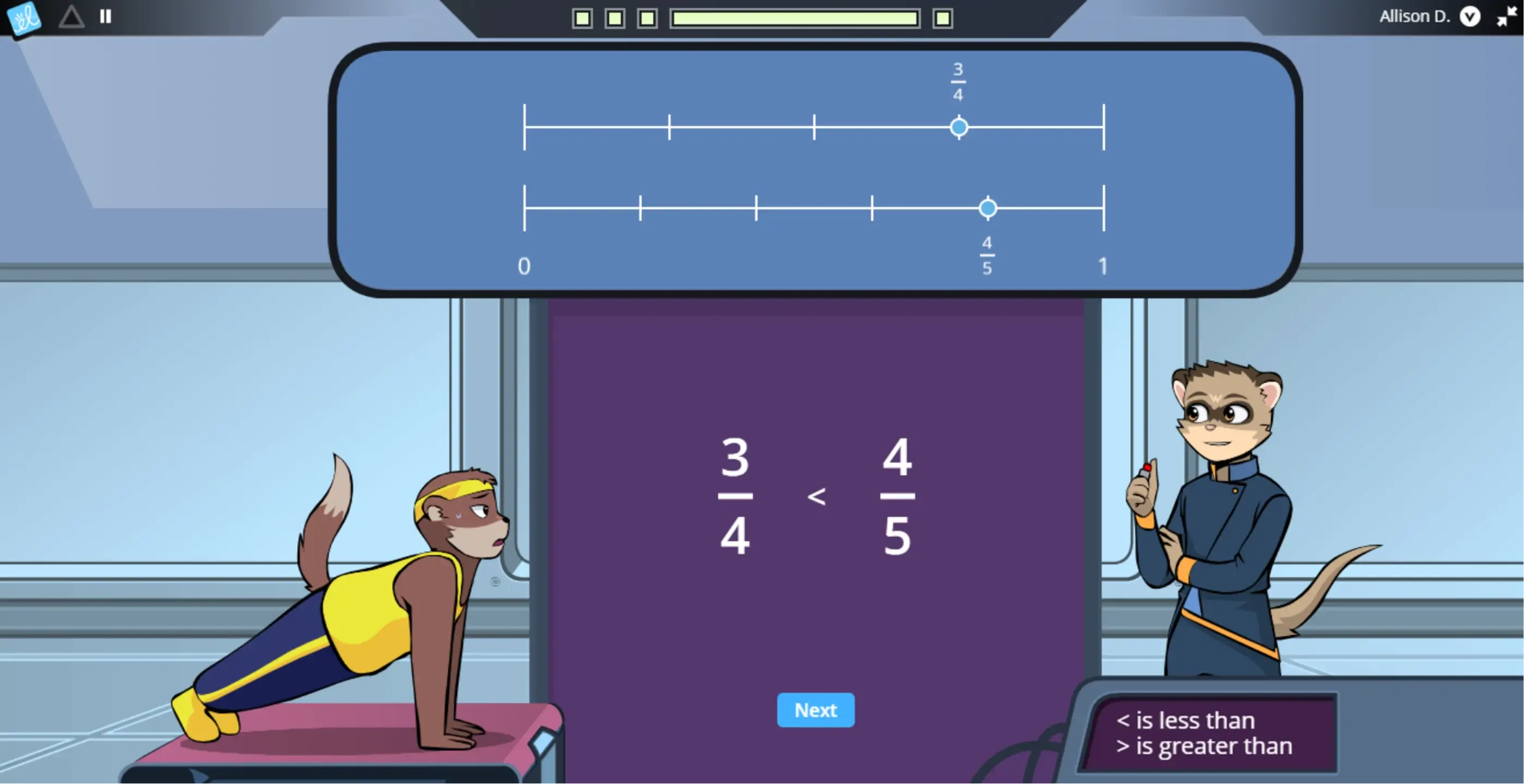
Given appropriate context, students can see that a length of 1/3 is less than a length of 1/2. They need to be able to visualize each fraction in relation to 1 in order to see the value of 1/2 in relation to 1/3. Students require a proper understanding of fraction magnitude (size) in order to accurately compare numbers. Students must understand how a numerator and denominator marry together to represent a single value (length). Visual representations, such as fraction strips, number lines, and shaded area models, can help students conceptually understand fraction magnitude. With ExploreLearning Frax, students learn that fractions are just like other numbers – with predictable names and locations on the number line – which prepares them to compare a fraction’s size to 1 and other fractions.
Fractions misunderstanding #2: Treating the numerators and denominators as whole numbers when adding fractions
When adding two fractions, it is common for students to add both numerators together and then both denominators together to find the sum. This misunderstanding often stems from a lack of fluency as students intuitively apply a “go-to” strategy they learned when adding whole numbers. With exposure to appropriate representations of fractions over time, students are more inclined to read the expression 1/4 + 1/4 as “one-fourth plus one-fourth.” They see each addend as two distinct numbers and are confident to write and say the sum as 2/4, or two-fourths, rather than the incorrect 2/8.
Common misconception:
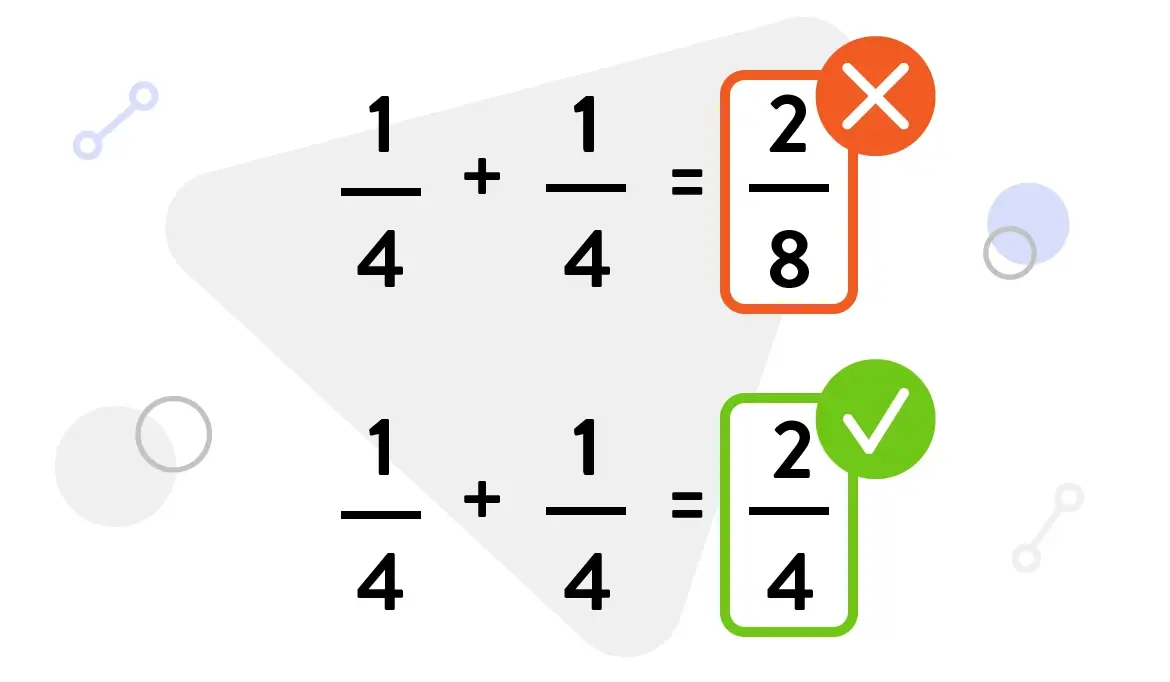
Fractions teaching solution #2: Emphasize unit fractions early and often
It's important to emphasize the value, meaning, and length of unit fractions early and often, just as you would when teaching students to count whole numbers. This helps students intuitively understand what the sum of two fractions with the same denominator represents. It is only when students understand fractions as numbers that they will better grasp other ways fractions can be used. Examples include subtracting fractions and reasoning about fractions using number line estimation skills, both of which are embedded throughout Frax. These skills ensure that students maintain and build on their strong number sense, which is vital for mature fraction work (and algebra readiness).
Fractions misunderstanding #3: Thinking fractions are best represented using pizzas and pies
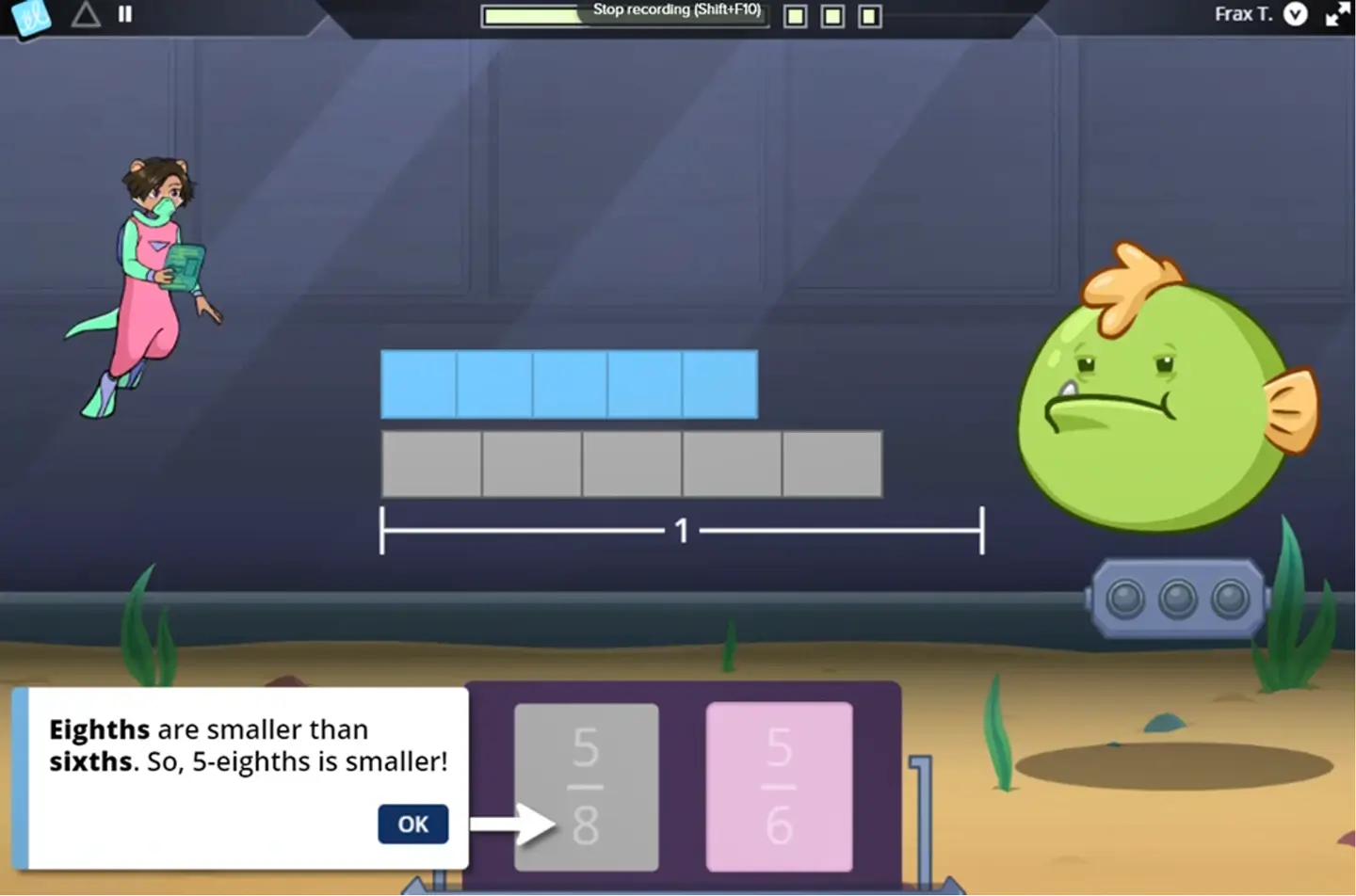
Pizza and pies are effective for helping students visualize the difference between fractions like 1/4 and 1/2. However, these models can only take students so far because they are difficult to interpret with precision as students attempt to represent mixed numbers and more complex fractions. Students can quickly begin to misinterpret the magnitude of fractions, too. If children cannot interpret the value of a fraction, then they will struggle to reason about them. When teachers ask students to compare two fractions using a model, they might automatically attempt to draw circular models and find it difficult to move past benchmark fractions (as in the example below). Appearing visually similar at first glance, a student might struggle to justify whether 4/6 or 3/5 is greater without a proper understanding of magnitude.
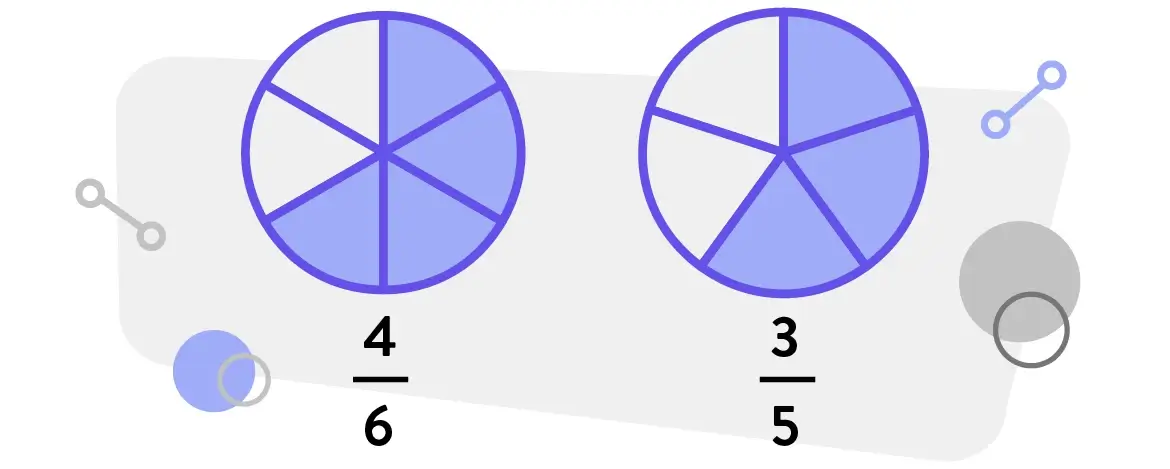
Fractions teaching solution #3: Incorporate the use of number lines when teaching fraction concepts
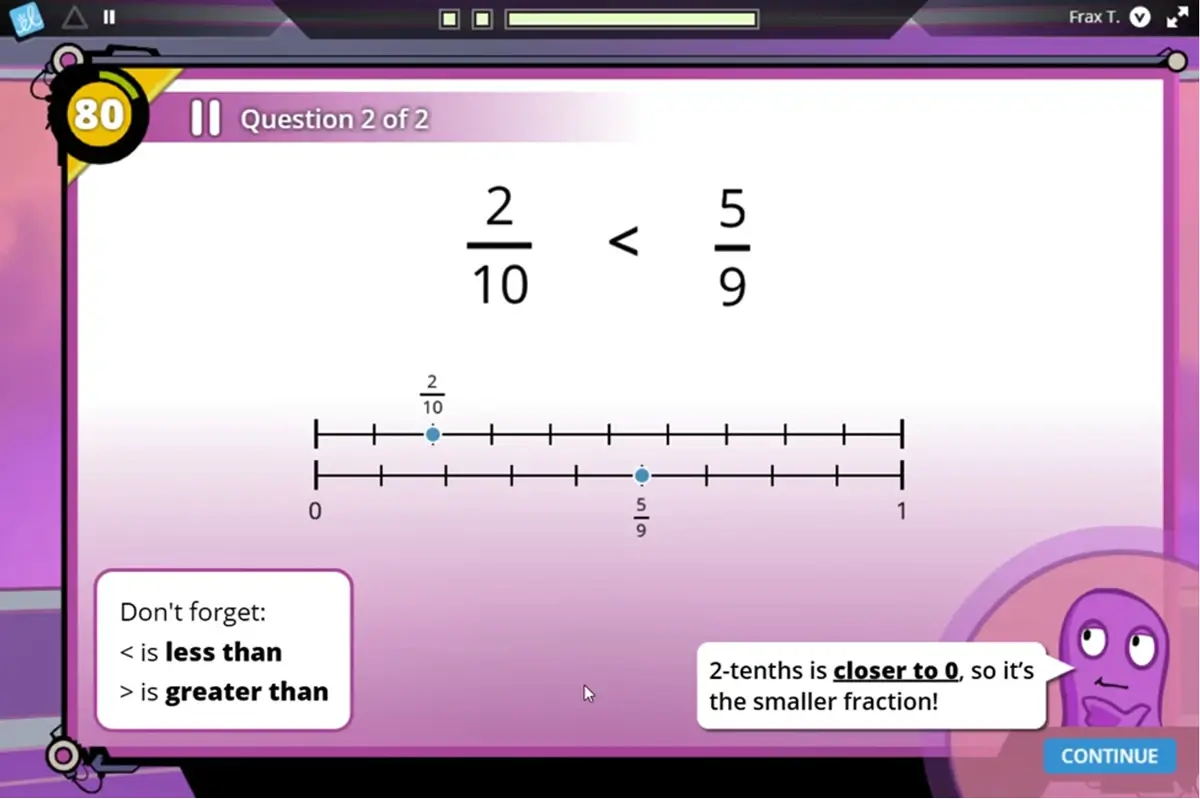
Number lines are increasingly recognized as the single most powerful and important representation for fractions content in elementary grades. Students learn to count the number of intervals between 0 and 1 and associate that number with the denominator. Then, they count the number of intervals between 0 and a particular point and associate that number with the numerator. Frax situates the number line as a key tool for students to rely upon, gently introducing the representation through various game-based interactions that focus on the meaning and comprehensibility of fractions. Along their Frax adventure, students progress through engaging missions to extensively practice all of the subskills required for effective use of a fraction number line.
Tackle these fraction challenges and more with Frax!

Sign up today for a 30-day free trial to access the game-based adaptive fractions solution for your classroom.
Try Today