Fractions on a Number Line: Overcoming Common Student Challenges

Why is it important to teach fractions on a number line?

A consensus is emerging in the educational research around fractions instruction: fractions should be taught using number lines. They are increasingly recognized as the single most powerful and important representation for fractions content in the elementary grades. In fact, “several interventions that focused on building fraction magnitude knowledge using number lines yielded better learning than regular school curricula” (Tian, 2021, p. 307). This trend doesn’t just hold for magnitude knowledge, however—the benefits accrue to learning fractions operations, such as addition and subtraction, as well (Jayanthi et al., 2021, p. 98).

Having an effective tool for learning fractions doesn’t just make elementary schoolers’ lives easier. As the key to unlocking a deeper understanding of fractions, number line competency helps students succeed well into the future. There is strong evidence to suggest that, even after controlling for common variables that affect math performance (like working memory, IQ, family income, or educational level), fractions knowledge at the end of grade 5 is a strong and unique predictor of success in high school mathematics (Siegler et al., 2012).

In fact, the number line has proven to be so effective in helping students deepen their understanding of fraction magnitude that the Department of Education’s Institute of Education Sciences included it as one of their two chief recommendations in the 2010 practice guide for fractions instruction (Siegler et al., 2010).
 

Why are number lines rarely used in classroom instruction?

Despite the clear student benefits of using number lines as the main fractions learning tool, why are they rarely used in the classroom?

As any experienced teacher will tell you, there can be a wide gulf between what research points to as a best practice versus what is actually doable in the classroom. Approaches that are researched and validated in one-on-one or small focus groups don’t always scale well to full-class instruction. This doesn’t reduce the efficacy of the method, nor should it detract from the importance of the research findings. Still, it does have implications for the real-world impact of methods that are found to be effective in experimental settings.

Many methods highlighted by the growing body of research around number-line-based instruction are challenging to implement in a traditional classroom. There are several reasons why good teachers might not shift their instruction towards a greater reliance on fraction number lines despite a strong commitment to following research-based best practices. Number lines are very difficult to teach and use in a classroom full of kids.

It’s important to frankly acknowledge these difficulties in order to successfully overcome barriers to implementation. Otherwise, number-line-based instruction risks the same fate as many other research-validated methods: an important finding that never gets traction in the real world of education.
 

What are the barriers to fractions instruction on a number line?

Let’s examine five of the most common roadblocks students face when working with fractions on a number line.
 

1. Fraction number lines are more variable than number lines representing whole numbers

   While students may be familiar with base ten number lines from skip counting and place value exercises in earlier grades, the notion of a number line with tick marks that do not represent “1” is new.

   This appears minor, but it’s actually a major shift in student thinking. Skip counting is precisely what its name implies: the student “skips” over sets of 1’s to the next number. Even so, the tick marks themselves always represent exactly the same value. In fact, it’s that very uniformity that allows students to develop reliable conceptual models of skip counting and, ultimately, multiplication.

   

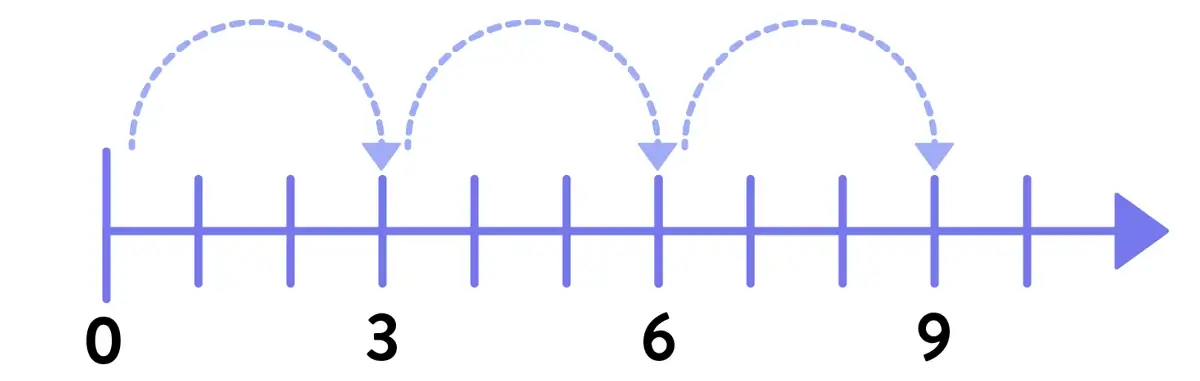
   Things change radically with fractions. Now, the distance between 0 and 1 remains constant, but the distance between the tick marks can change substantially based on the denominator value of the fraction.

   

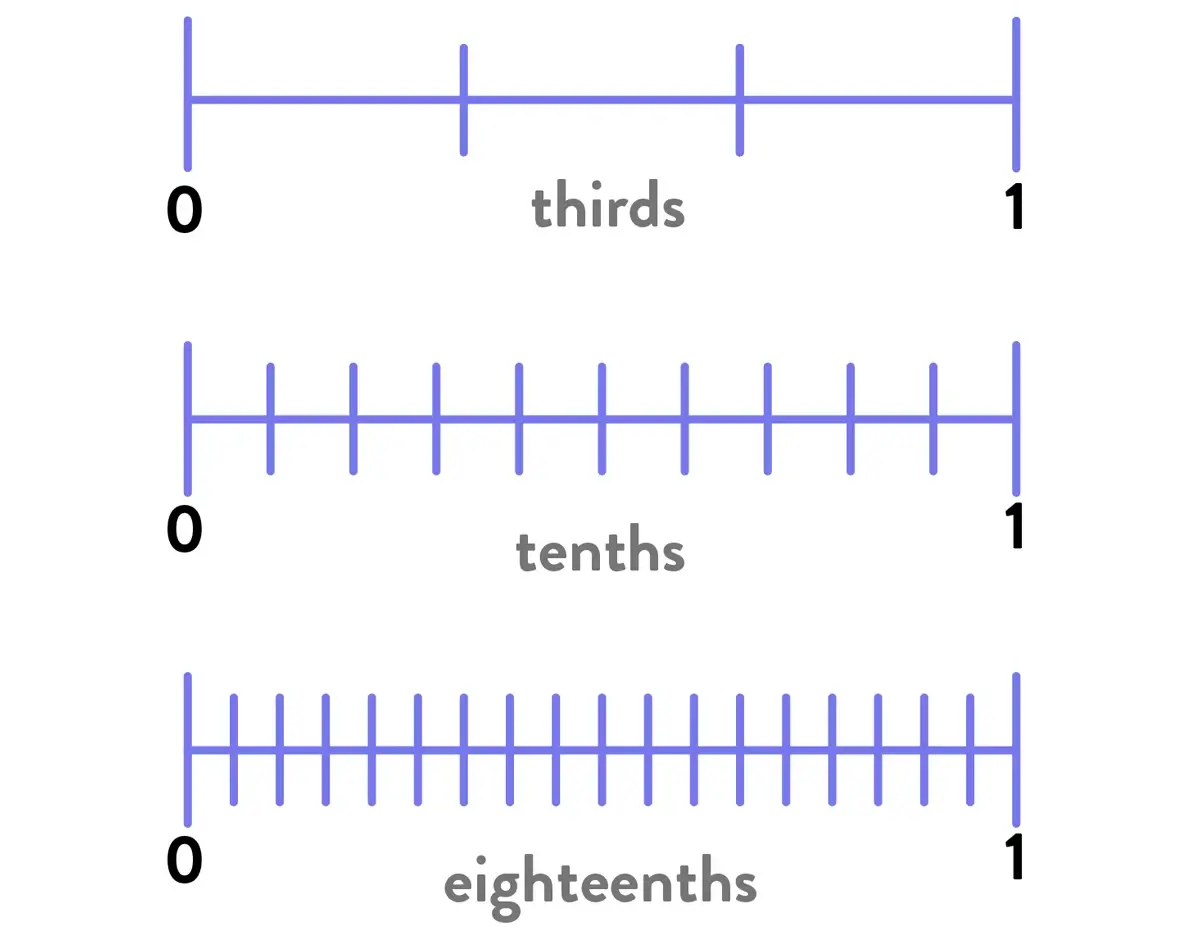
   This lack of predictability can be confusing for many students, especially when it comes on the heels of – or concurrently with – using number line representations for whole number work.
    

2.  Students lack experience with ruler measurement 

   Most students have little to no hands-on experience with measurement outside of the classroom. In the United States, ruler practice is often one of the only places a child gets hands-on experience working with a non-decimal (i.e. non-base-10) number line. However, few students today engage in activities that would provide them with substantial practice and familiarity with ruler measurement.

   By the time elementary students approach fractions instruction, most of their previous exposure to fractions on a number line is limited to their previous math and science lessons with measurement components – hardly a robust experience set. Is it any wonder why measurement and number line work are two of the most challenging topics to cover for most math teachers? They go hand-in-glove.
    

3.  Number lines can become an overwhelming visual stimulus, leading to a high “cognitive load” 

   Fraction number lines can quickly become a sea of visual information. Notice how much attention to detail it requires to determine the following point’s value in this example.

   

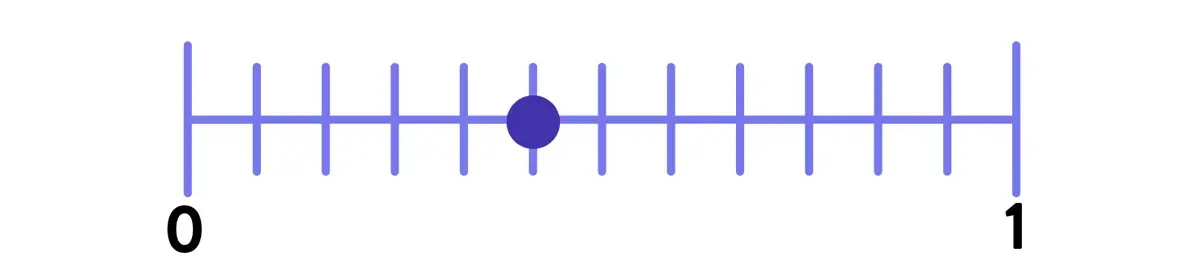
   Compare that visual density (and cognitive effort) of the number line to the much more visually intuitive shaded area model for the same fraction, ⁵/₁₂.

   

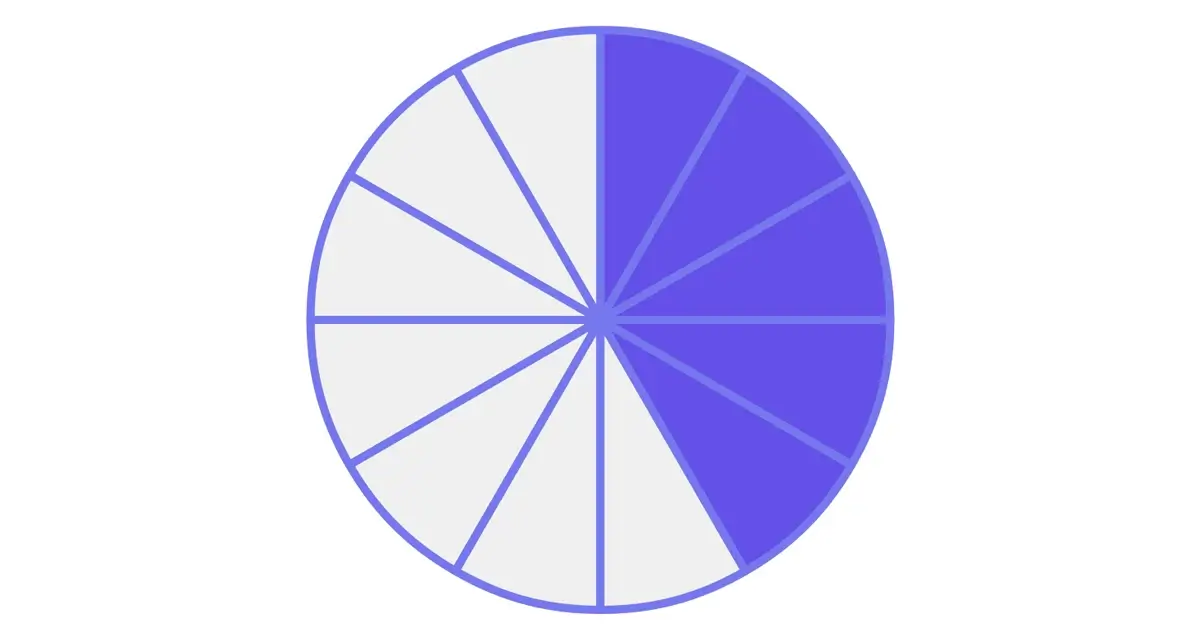
   Notice how much easier it is to interpret the shaded area model? You can mentally parse the circle into halves, quarters, and finally, twelfths, and then count five shaded pieces. It takes much less concentration and mental energy to identify the relevant pieces of information.

   It’s a small wonder that teachers with limited time – and even more limited student attention and mental energy – tend to default to using these less demanding representations… even when they really aren’t the best tool for the job.
    

4.  Interpreting fractions on a number line requires a unique set of subskills 

   What is it about shaded area models that feels much more “intuitive” to students? For learners unaccustomed to number lines, shaded area models are more approachable because of their familiarity and comparative visual simplicity. Consider the following example of a shaded area model for ⁵/₈.

   

   The space representing “1” is clearly visible, and the partitions are “bulkier.” Additionally, many shaded area models present partitions as an array, a familiar representation for students thanks to their work in multiplication. The numerator (five) is clearly represented by differentiated coloring, which is easy to identify and count.

   Basically, saying that shaded area models are “intuitive” is shorthand for the fact that they require less cognitive overhead for students. Most students simply haven’t had the opportunity to develop the micro-skills associated with interpreting number lines. A lack of familiarity with (and practice of) those skills makes number line work more attention-intensive and laborious.

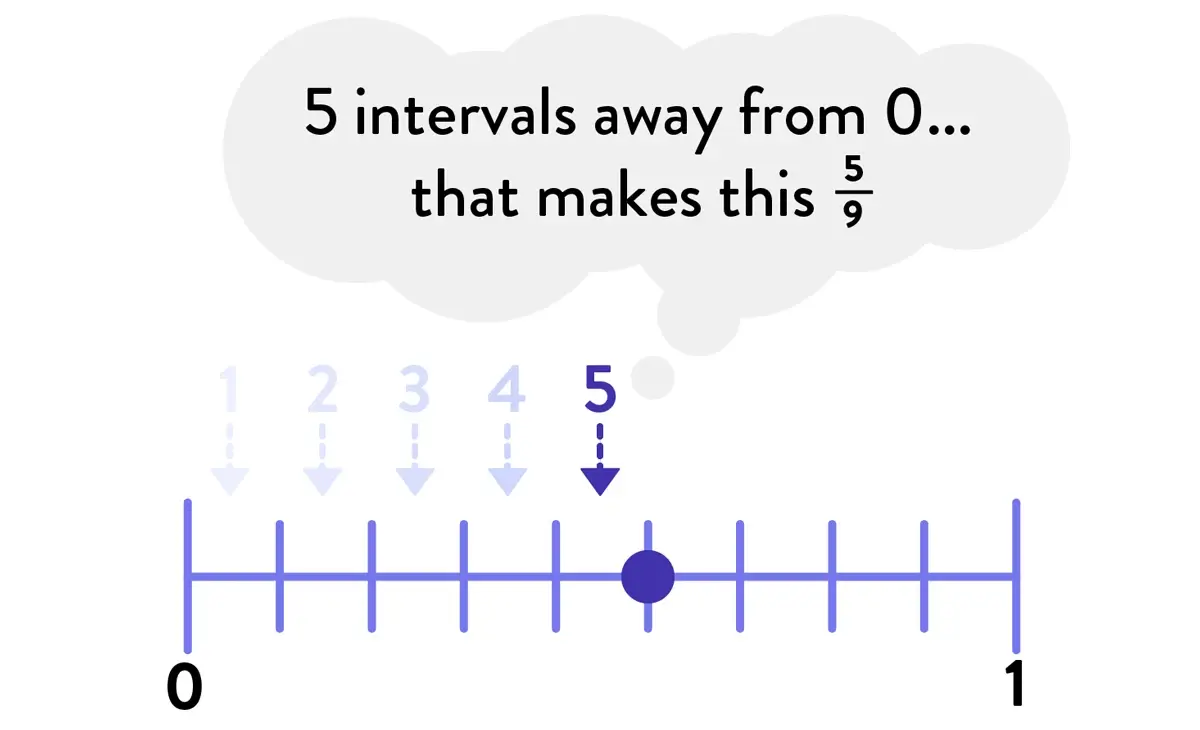
   What are the subskills that make number line work so much more intensive for students who are initially exposed to them? Look at the following number line representation.

   

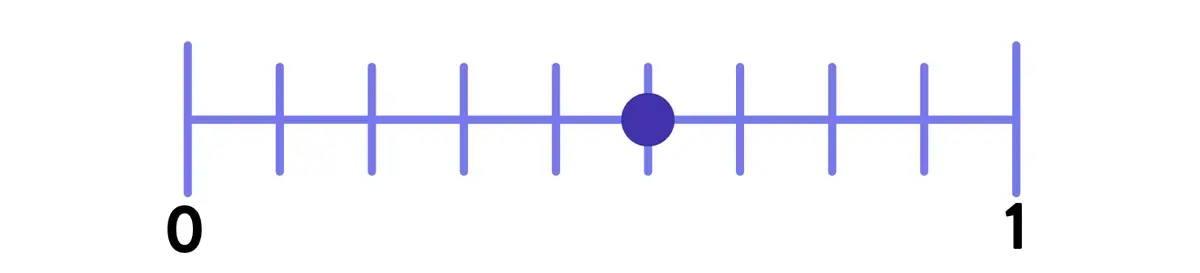
   In order to correctly interpret the value, a student needs to do the following:

   • Differentiate between the tick marks (visually salient) and intervals (not visually salient) and focus attention on the intervals only.

     

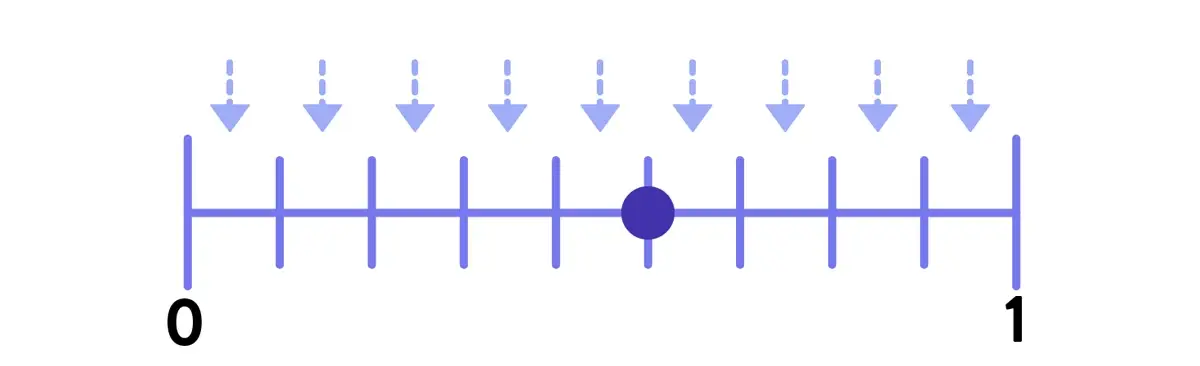
   • Count the number of intervals between 0 and 1. In this example, the student finds there are nine intervals.

     

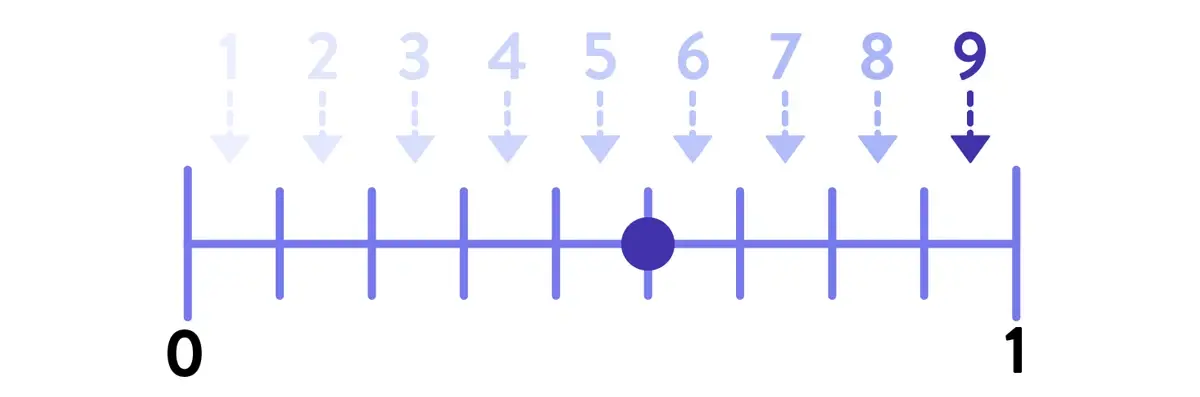
   • Bonus skill for fractions greater than 1– A student must ensure they’ve only counted the intervals between 0 and 1!

     

   • Associate the number of intervals between 0 and 1 with the denominator.

     

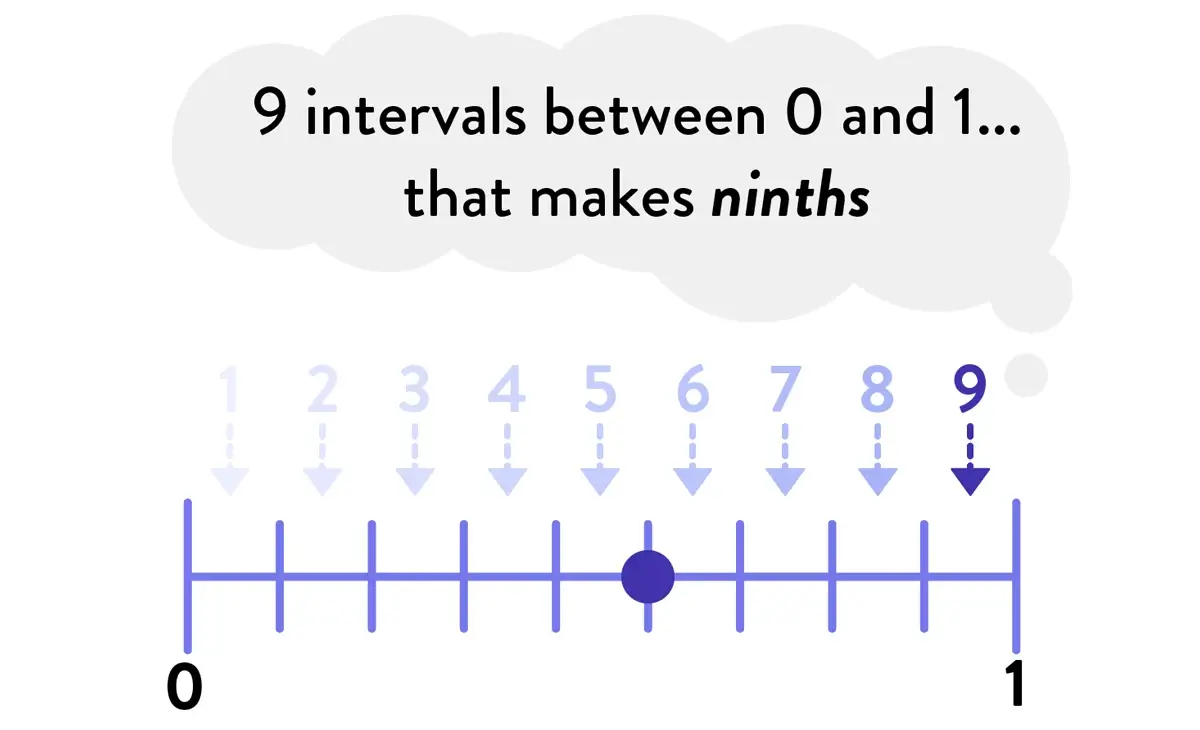
   • Finally, count the number of intervals between 0 and the point, and associate that with the numerator.

     

   • A student’s (or an adult’s!) brain needs to build these skills over time, akin to doing conditioning for a sport. Until they’ve done so, number lines will be perceived as “difficult” or “confusing,” and there will be a natural resistance to working with them. The subconscious (or conscious) choice by students and teachers will be to default back to shaded area models because they’re more “intuitive” or “easier to use.”

   
   

   It’s always hard to convince someone to use a tool they’re not comfortable with, even if they do believe it will be better for them in the long run. The fact that the familiar (but less useful) tool is easier to use today generally outcompetes the desire to learn a new tool that will be more useful tomorrow. Doubly so if you’re already stressed about the task you’re working on.

   Bottom line: there’s a vicious cycle with this representation where it’s perceived as difficult by students (and teachers), leading to a lack of practice with number lines, leading to a more entrenched perception of difficulty.
    

5.  Lack of just-in-time remediation while learning to use the number line representation 

   Students who are still learning the essentials of number line representations require immediate feedback on mistakes. Otherwise, they are prone to cement conceptual misunderstandings as they repeatedly draw incorrect conclusions about the representation.

   Neuroplasticity works for good or ill. As one veteran teacher stated, “Practice makes permanent.” The danger is that during whole class instruction on this topic, students might practice the wrong thing repeatedly while the teacher helps other students elsewhere in the classroom.

   The unfortunate reality of a classroom, however, is that there is no easy method for providing the necessary kind of simultaneous, just-in-time feedback to students required to adequately learn this topic. There’s simply no lesson design – no matter how original or inspired – that can simultaneously and immediately address all of the errors encountered by a classroom full of students as they work to learn this conceptual tool. Unlike other topics, there is little scope to create lessons with meaningful “self-check” or “partner check” elements, especially when students are first learning how to understand and navigate the representation.

   The eventual outcome is that teachers tend to naturally (and understandably!) move quickly through their number line content in order to invest precious instructional time where they can more adequately address the needs of their entire class using the instructional tools available to them.

    And thus the cycle continues: another class of elementary students misses out on the potent impact of number line learning for fractions… 
      

Overcoming these barriers to implementation

Understanding barriers to teaching and implementing fractions on a number line is the first step in helping teachers find effective ways to get this powerful tool into the hands of students. However, understanding the challenges is only the first step. What can be done to overcome them?

There are several things a teacher can do to mitigate the difficulty of teaching fractions on number lines. While the following suggestions may not eliminate all of the challenges, they can certainly help:

• Dedicate sufficient instructional time to allow for the difficulty of the representation
• Focus student attention on intervals, not tick marks
• Design lessons that leverage small-group instruction
• Use online resources to reduce the time gap between students’ mistakes and remediation
   

Frax eliminates the barriers to teaching fractions on a number line

ExploreLearning Frax is an adaptive, game-based fractions instructional tool that eliminates these barriers to effective implementation. Frax puts this powerful tool squarely within reach for all students. Taking its cues from the clear research around effective fractions instruction, Frax uses the number line as the central representational tool students encounter. They are gently introduced to number lines through a variety of fun, game-based interactions that focus on the meaning and comprehensibility of the representation.

Along their Frax adventure, students progress through missions to extensively practice all of the subskills required for effective use of a fraction number line.

Focusing on and counting intervals

 
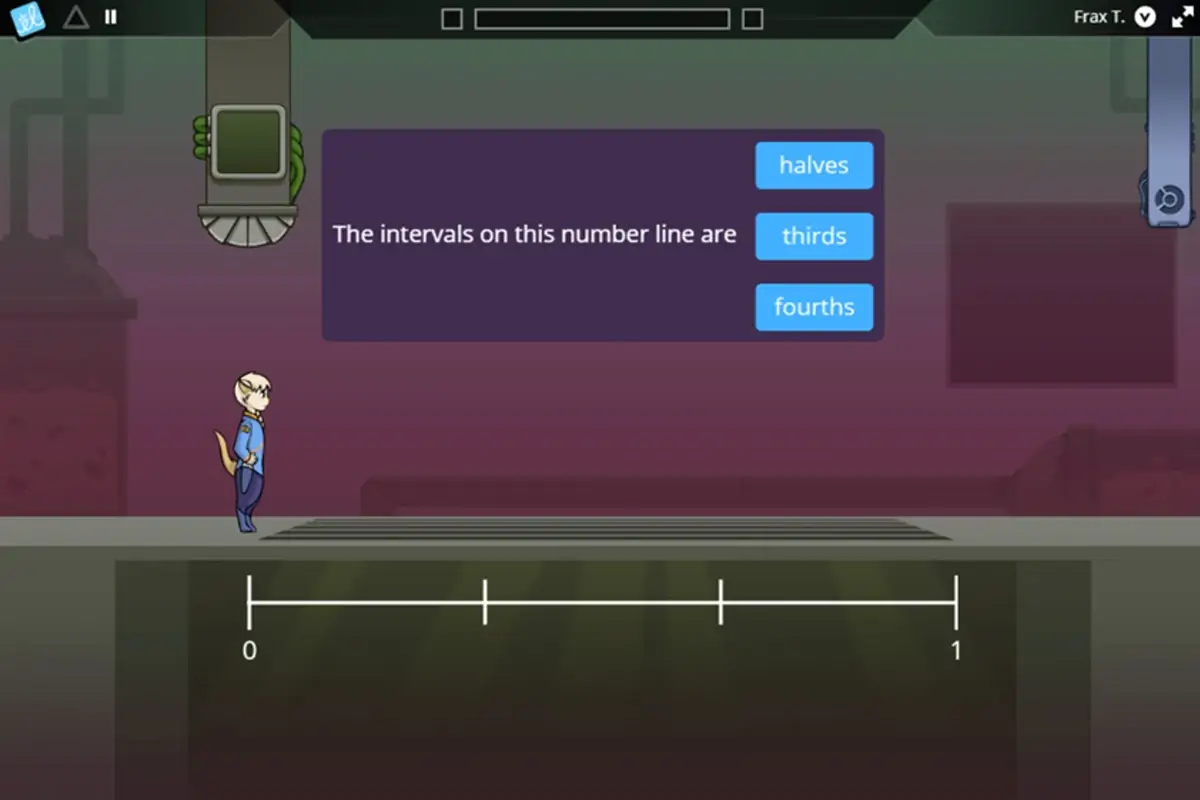
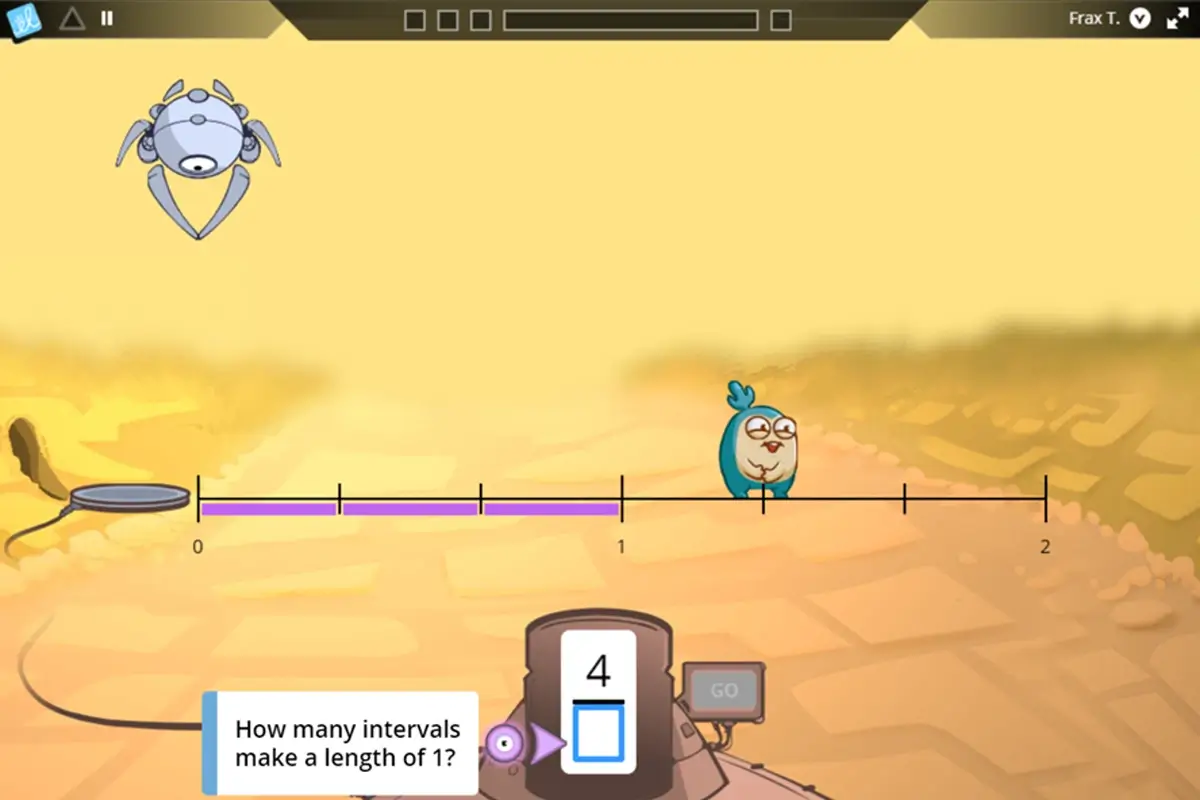
 Identifying the 0-1 space for fractions greater than 1.

 
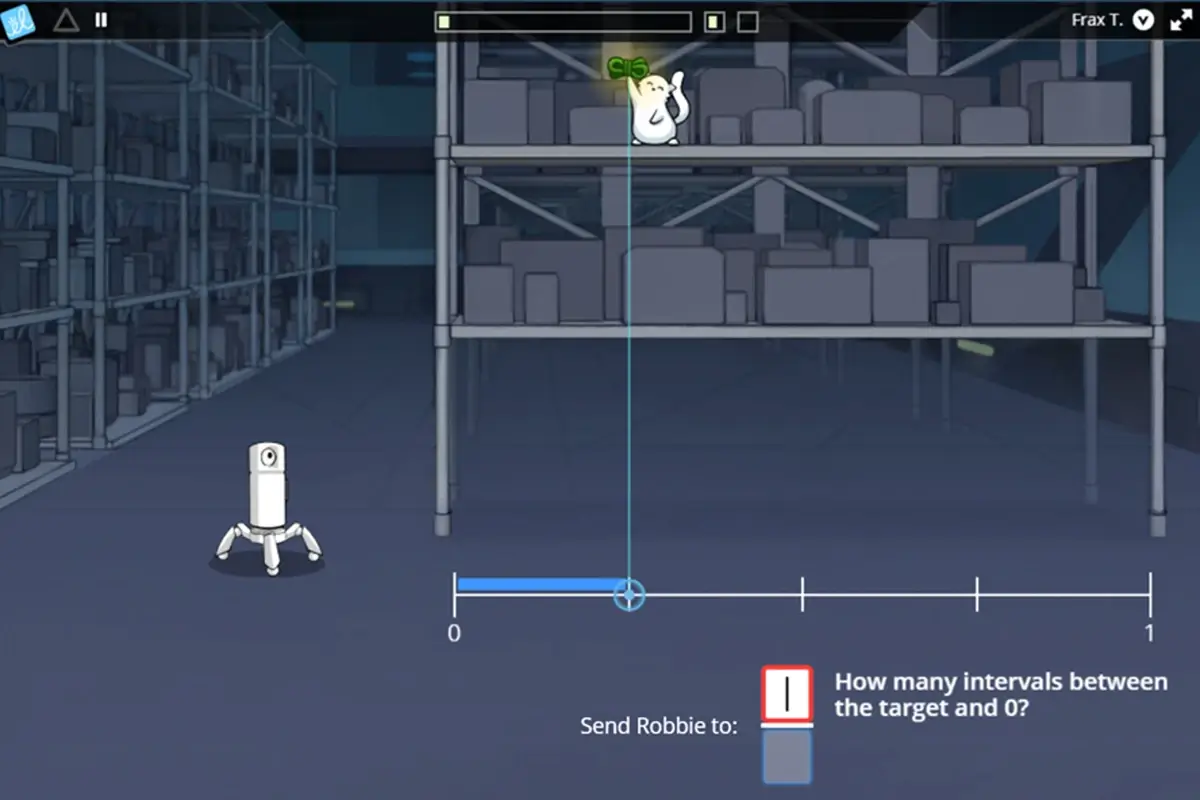
 Counting the number of intervals from 0 to the point. 

 
The 1-to-1 nature of Frax’s web-delivered content means that an entire classroom full of students can simultaneously receive the benefits of research-based methods in an environment where each student’s individual mistakes and misconceptions can be immediately addressed (and Frax is way more fun than a worksheet!).

Thanks to engaging games and instantaneous feedback, students wind up doing significantly more practice problems with Frax than they would with paper-based activities. Not only that, but each student receives the just-in-time remediation and adaptive question selection they need for their current level of proficiency – not their neighbor’s.

Using Frax allows teachers to give students precisely the kind of research-validated experience we all long to provide. Additionally, Frax gives teachers the opportunity to work individually with students who may still be struggling and to pursue mathematical conversations and group-based activities to deepen understanding.
 

Teachers + Frax make a powerful combination in helping all students master this difficult topic!

Help students 3-5 build deep conceptual fractions understanding.

 Try Frax Today