Fraction Types and Terms (and a Holistic Perspective on Fractions)

Proper, improper, equivalent, benchmark…there’s a lot of terminology surrounding fractions. With so many fraction terms, math can often seem like another language to students and teachers alike. How can you help students understand these “types” of fractions during a busy classroom math block? Keep reading for simple definitions and strategies to try today!
How “parts of a whole” can lead students astray
People often think of fractions as parts of a whole or slices of a pie. This makes sense when looking at something that is less than one. 7/9 of the pizza is pepperoni. 10/15 of the students are wearing red. 2/3 of the girls own dogs.
But what about the fraction 11/9? Enter confusion. If students only think of fractions as parts of a whole, they might think it's not even possible for a fraction to be greater than 1.
So, what are the types of fractions? In reality, all fractions are numbers, each with magnitude (size) and a location on the number line. Consider the different “types” of fractions and terms as simply as how each fraction is expressed and understood in different contexts. These fraction terms are categories that fractions can be grouped into. Recognizing these distinctions helps students grasp more than just how to “do” fractions, but truly develop a conceptual understanding of fractions.
Why it’s important to teach fractions as numbers
First, students must understand how a numerator and denominator work together to create a single value (length). Then, they will be able to locate and find fractions on the number line in relation to other numbers. With a strong fraction number sense, students can apply their knowledge to advanced work with fractions, such as comparing fractions, decomposing fractions, fraction arithmetic, and eventually algebra.
ExploreLearning Frax, an adaptive and individualized fractions program, uses research-based methods to help students develop this foundational understanding of fractions as numbers.
Common fraction terms, concepts, and their definitions
All the “types” of fractions will become more intuitive for students to grasp once they understand fractions as numbers. A fraction is still a fraction whether it is less than, equal to, or greater than one. Let’s look at the common fraction terms students will encounter.
Unit fractions
Some of the first fractions students interact with are unit fractions, or fractions with a numerator of 1. Fractions like 1/2, 1/3, 1/4, and 1/10 are all examples of unit fractions.
Benchmark fractions
Benchmark fractions are “common” fractions that help provide students with reference points as they place and compare other fractions. Examples include 1/2, 1/3, 1/4, 2/3, and 3/4. Benchmark fractions serve as mental anchors on the number line and are especially useful in real-life reasoning and problem-solving.
Proper fractions
A proper fraction has a numerator less than its denominator (like 3/4), which means the fraction is between 0 and 1.
Fractions greater than one (improper fractions)
Fractions greater than one have a numerator greater than the denominator. Since fractions are numbers too, they can be greater than one (just like any “regular” number). For example, 6/6 is equivalent to 1. If students count by sixths, they encounter 7/6, 8/6, and beyond. All of these are fractions greater than one.
Fractions greater than one can be rewritten as mixed numbers. For example, students could rewrite 8/6 as the mixed number 1 2/6.
You might also encounter the term improper fractions in textbooks or curricula to describe a fraction with a greater numerator than the denominator. It’s important to address this term with students in case they encounter it on assessments, but there is no need to emphasize it during instruction. Once students understand that fractions are numbers, it becomes much more intuitive that numbers (including fractions) can be greater than one.
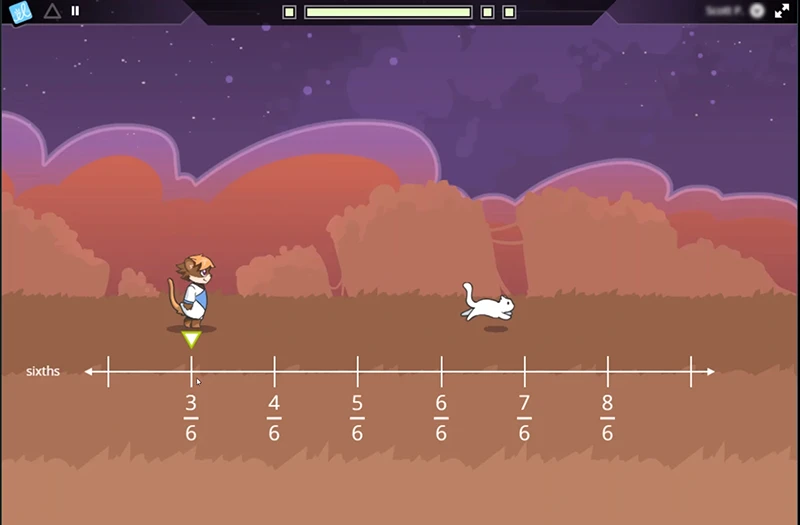
Students interact with fractions greater than 1 in the game-based fractions program Frax.
Mixed numbers
Mixed numbers are fractions greater than one that are written as a whole number and a fraction. For example, the fraction 13/8 can be rewritten as the mixed number 1 5/8.
Decimal fractions
Fractions like 1/10 or 3/100 are called decimal fractions. These fractions have a denominator with a power of 10, such as 100, 1,000, or 10,000. Decimal fractions tie directly into the base-ten system and can be converted and easily written as decimals. For example, 1/10 = “one tenth” = 0.1. The fraction 88/100 is “eighty-eight hundredths” or 0.88.
Fraction pairs
As students progress in understanding, they develop the confidence to understand how two fractions relate to one another.
Equivalent fractions
Equivalent fractions are two different fractions that have the same value. Think of them as different ways of measuring the same length! Equivalent fractions lie at the same location on the number line.
It’s helpful to remind students that equivalent fractions represent the same value, even if they look different. For example, even though 2/3 and 4/6 have different denominators, they have the same position on the number line. Teaching equivalence supports simplifying fractions, comparing them, and understanding proportional reasoning.
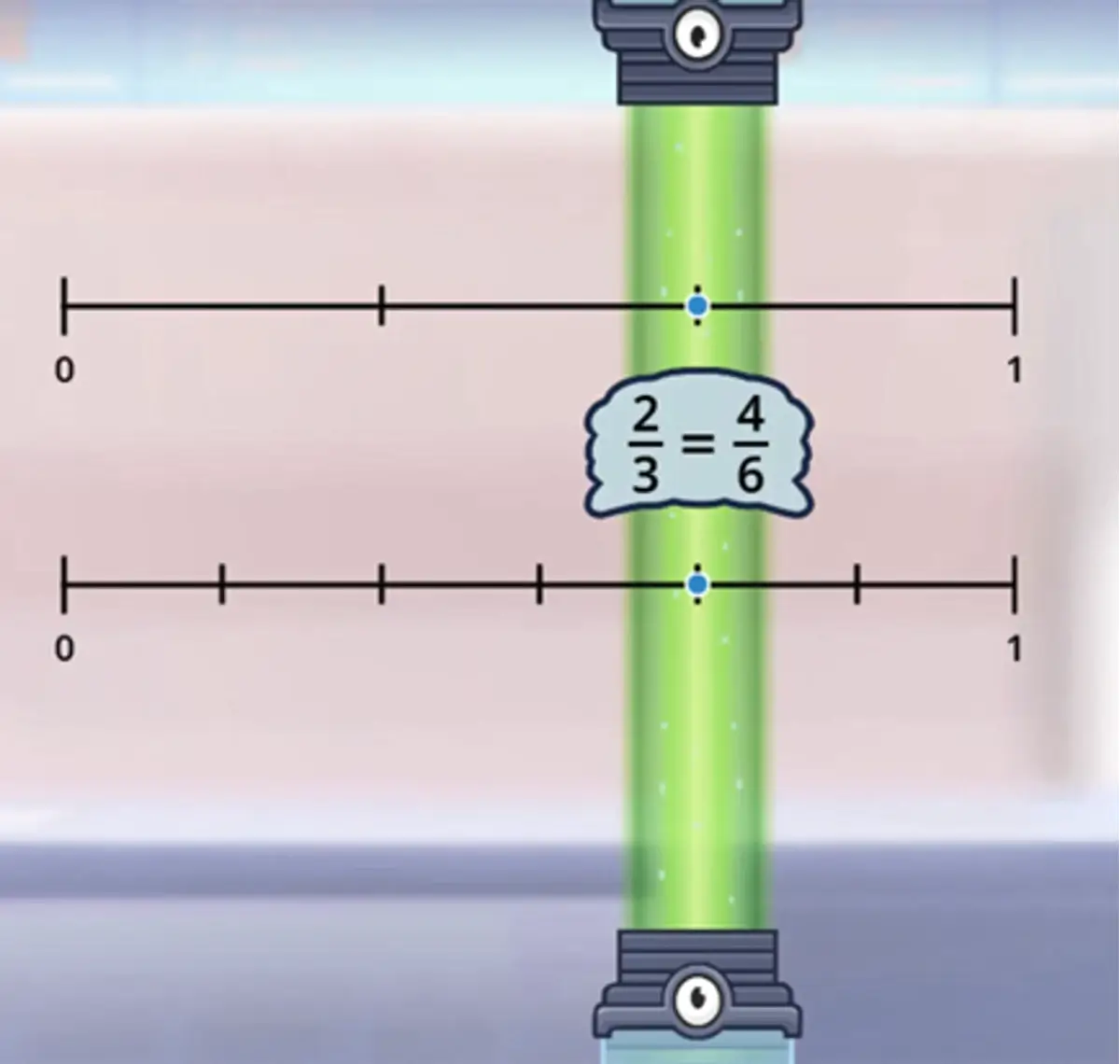
Comparing fractions
Since fractions are numbers, students can compare them to determine if a fraction is less than, equal to, or greater than another. To compare fractions, students often use strategies such as finding common denominators, converting to decimals, or using benchmark fractions. These strategies build a strong foundation for proportional reasoning and algebra.
Operations with fractions
What else can students do with a strong understanding of fractions as numbers?
Adding and subtracting fractions
Just like numbers, students can add and subtract fractions. To complete these calculations, students must understand how to regroup, convert between forms, find a common denominator, and sometimes simplify or rename fractions.
Multiplying and dividing fractions
Similarly, students can also multiply and divide fractions. The fractions might have different denominators, but these advanced operations are possible once students can locate fractions on the number line.
Teaching for a true understanding of fractions
Lay strong classroom foundations today to help your students master fractions.
Fractions on the number line
Research shows that the most effective learning occurs when students develop an understanding of fractions using visual models like length models and number lines. Placing fractions on a number line reinforces their identity as numbers. It helps students visualize magnitude, see equivalence, and understand operations like addition and subtraction as movements along the number line.
Frax uses visual representations like length models to introduce fractions on a number line through carefully scaffolded tasks. Frax gradually incorporates number lines through various fun, game-based interactions that focus on the meaning and comprehensibility of the representation, ensuring students understand intervals and fraction magnitude before they locate and place fractions on a number line.
Plotting fractions
When working with number lines, you might hear the expression “plotting fractions.” In the elementary years, most references to plotting fractions are likely related to placing or positioning fractions on the number line. However, asking students to “plot fractions” can be confusing and misleading for elementary learners new to fractions. Try adjusting your fraction vocabulary and ask students to find, locate, or represent a fraction on a number line instead.
Deepen fractions understanding with Frax
By exploring these fraction terms and operations, you will give your students a strong, flexible understanding of fractions, equipping them for success with more advanced math and everyday applications. Combining your classroom instruction with Frax allows students to understand fractions not as disconnected terms or operations, but instead as numbers that live on the number line.
Frax is a zero-entry program that allows all students to improve their fraction knowledge and build confidence as they complete carefully scaffolded missions while having fun in a space-themed galaxy setting. Thanks to adaptive learning, students practice fraction concepts at their level and receive feedback to help them progress. Frax also helps teachers be more effective, with tools like reporting, progress monitoring, and a variety of offline activities that reinforce number line concepts and assess understanding.
For example, with Frax, a student comes to understand that 9/9 is equivalent to 1. From there, they can reason that 8/9 is barely less than 1 and 10/9 is barely more than 1. While 8/9 is in the bucket of "proper fractions" and 10/9 is in the bucket of "fractions greater than one," the student comes to understand that there’s not much difference between them once they have a foundational understanding of fractions as numbers.
Teach advanced fractions concepts with Frax
Coming in fall 2025, expanded Frax Sector 3 will help students level up their learning with all-new adventures that extend and deepen their understanding of fractions. Students will use the foundations built in Sectors 1 and 2 to navigate new worlds and develop a strong and durable mastery of grade 5 fraction arithmetic.
Sector 3 areas of focus:
- Adding and subtracting fractions with unlike denominators
- Multiplying fractions
- Dividing fractions
- Simplifying fractions
- Converting between mixed numbers and improper fractions
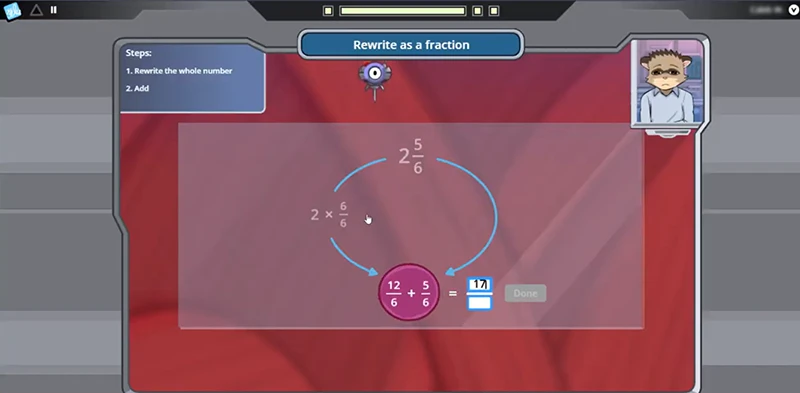
In Frax Sector 3, students practice converting between mixed numbers and fractions greater than 1.
Research-based for real results
Are you ready to make fractions make sense in your classroom? Try Frax today, and your students can uncover a variety of fraction concepts while having fun.